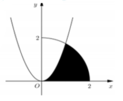
Gọi H là hình phẳng giới hạn bởi P y = 3 x 2 , cung tròn y = 4 - x 2 0 ≤ x ≤ 2 và trục hoành (phần tô đậm trong hình vẽ). Thể tích của khối tròn xoay thu được khi quay H xung quanh trục Ox bằng
A. 34 15
B. 34 π 15
C. 43 15
D. 43 π 15
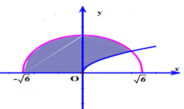
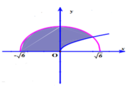
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x , cung tròn có phương trình y = 6 - x 2 ( - 6 ≤ x ≤ 6 ) và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng H quanh trục
![]()
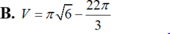
![]()
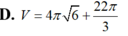
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x , cung tròn có phương trình y = 6 - x 2 - 6 ≤ x ≤ 6 và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng H quanh trục
A. V = 4 π 6 + 22 π
B. V = π 6 - 22 π 3
C. V = 8 π 6 + 11 π
D. V = 4 π 6 + 22 π 3
Chọn D.
Phương pháp: Chia miền cần tính thể tích làm 2 phần.

Gọi (H) là hình phẳng giới hạn bởi (P): y = 3 x 2 cung tròn y = 4 - x 2 ( 0 ≤ x ≤ 2 ) và trục hoành (phần tô đậm trong hình vẽ). Thể tích của khối tròn xoay thu được khi quay (H)xung quanh trục Ox bằng
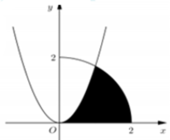
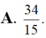
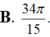
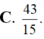
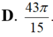
Cho (H) là hình phẳng giới hạn bởi Parabol y = 3 x 2 , cung tròn có phương trình y = 4 − x 2 0 ≤ x ≤ 2 và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng:
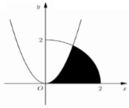
A. 4 π + 3 12 .
B. 4 π − 3 6 .
C. 4 π + 2 3 − 3 6 .
D. 5 3 − 2 π 3 .
Đáp án B
Xét phương trình tương giao:
3 x 2 = 4 − x 2 ⇔ 3 x 4 = 4 − x 2 ⇔ x 2 = 1 ⇒ x = ± 1 x 2 = − 4 3 ( L ) S = ∫ 0 1 3 x 2 d x + ∫ 1 2 4 − x 2 d x = 3 x 3 3 1 0 + S 2 S 2 : x = 2 sin t , t ∈ ( − π 2 ; π 2 ) ⇒ d x = 2 cos t d t S 2 : ∫ π 6 π 2 2 cos t .2 cos t d t = ∫ π 6 π 2 4 cos 2 t d t = 2 ∫ π 6 π 2 ( 1 + cos 2 t ) d t = 2 [ t + sin 2 t 2 ] π 2 π 6 = 2 π 3 − 3 2 ⇒ S = 3 3 + 2 π 3 − 3 2
Cho (H) là hình phẳng giới hạn bởi Parabol y = 3 x 2 , cung tròn có phương trình y = 4 - x 2 0 ≤ x ≤ 2 và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng:
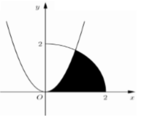
A. 4 π + 3 12
B. 4 π - 3 6
C. 4 π + 2 3 - 3 6
D. 5 3 - 2 π 3
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = x cung tròn có phương trình y = 6 - x 2 ( 6 ≤ x ≤ 6 ) và trục hoành (phần gạch chéo trong hình vẽ). Tính thể tích V của vật thể xoay tròn sinh bởi hình phẳng D khi quay D quanh trục Ox.
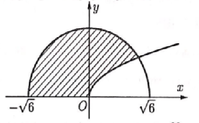
A. V = 8 π 6 - 2 π .
B. V = 8 π 6 + 22 π 3 .
C. V = 8 π 6 - 22 π 3 .
D. V = 4 π 6 + 22 π 3 .
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 , cung tròn có phương trình y = 4 − x 2 (với 0 ≤ x ≤ 2 ) và trục hoành (phần tô đậm trong hình vẽ).
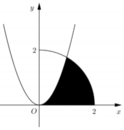
Diện tích của (H) bằng
A. 4 π + 3 12 .
B. 4 π − 3 6 .
C. 4 π + 2 3 − 3 6 .
D. 5 3 − 2 π 3 .
Đáp án B.
Phương trình hoành độ giao điểm là:
3 x 2 = 4 − x 2 ⇒ 0 ≤ x ≤ 2 3 x 4 = 4 − x 2 ⇔ x = 1.
Dựa vào hình vẽ ta có:
S = ∫ 0 1 3 x 2 d x + ∫ 1 2 4 − x 2 d x = 3 x 3 3 1 0 + I 1 = 3 3 + I 1
Với I = ∫ 1 2 4 − x 2 d x , sử dụng CASIO
hoặc đặt x = 2 sin t ⇒ d x = 2 cos t d t
Đổi cận
x = 1 ⇒ t = π 6 x = 2 ⇒ t = π 2 ⇒ I 1 = ∫ π 6 π 2 4 − 4 sin 2 t . c o s tdt = ∫ π 6 π 2 2 1 + c o s 2 t d t = 2 t − sin 2 t π 2 π 6
⇒ I 1 = 1 6 4 π − 3 3 . Do đó S = 4 π − 3 6 .
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 cung tròn có phương trình y = 4 - x 2 (với 0 ≤ x ≤ 2 ) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
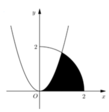
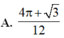
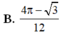
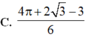
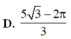
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 , cung tròn có phương trình y = 4 - x 2 (với 0 ≤ x ≤ 2 ) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
A. 4 π + 3 12
B. 4 π - 3 6
C. 4 π + 2 3 - 3 6
D. 5 3 - 2 π 3
Phần diện tích giới hạn bởi đường x = 4 - y 2 ; x = y 3 ; y = 0; y = 3 nên diện tích cần tìm là
S = ∫ 0 3 4 - y 2 - y 3 d y rồi dùng máy tính cầm tay để kết luận.
Đáp án cần chọn là B