Hình chóp tứ giác đều S A B C D có AB = a; góc giữa (SCD) và (ABCD) bằng 60 ° . Tính diện tích xung quanh ( S x q ) của hình chóp
A. S x q = 2 a 2 2
B. S x q = a 2 3
C. S x q = 2 a 2 3
D. S x q = 2 a 2
Những câu hỏi liên quan
Cho hình chóp tứ giác đều S. ABCD có cạnh AB=10cm. Cạnh bên SA=12cm a) tính đường chéo AC b) tính đường cao SO c) tính thể tích hình chóp
Khẳng định nào sau đây là sai?
Các hình chóp sau đây luôn có các đỉnh nằm trên một mặt cầu:
A. Hình chóp tam giác B. Hình chóp ngũ giác đều
C. Hình chóp tứ giác D. Hình chóp đều n-giác.
Chọn C.
Điều kiện để hình chóp nội tiếp được trong một mặt cầu là đáy của nó nội tiếp trong một đường tròn. Một tứ giác bất kì chưa chắc nội tiếp trong một đường tròn.
Đúng 0
Bình luận (0)
Chọn C vì điều kiện để hình chóp nội tiếp được trong một mặt cầu là đáy của nó nội tiếp trong một đường tròn. Một tứ giác bất kì chưa chắc nội tiếp trong một đường tròn.
Đúng 0
Bình luận (0)
Khối chóp tứ giác S.ABCD có đáy là hình bình hành. Có bao nhiêu mặt phẳng cách đều cả 5 điểm S, A, B, C, D?
A. 5
B. 11
C. 9
D. 3
Có 5 mặt phẳng cách đều 5 điểm S, A, B, C, D:
Mặt phẳng đi qua 4 trung điểm của 4 cạnh bên: có 1 mặt.
Mặt phẳng đi qua tâm O và song song với từng mặt bên : có 4 mặt như vậy
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD. Số mặt phẳng qua điểm S cách đều các điểm A, B, C, D là
A. 4
B. 2
C. 3
D. 1
Đáp án C
Có 3 mặt phẳng. 2 mặt phẳng là các mặt đi qua điểm S và qua các đường trung trực của AB và AD.1 mặt phẳng qua S và song song với mặt phẳng (ABCD)
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S . A B C D . Số mặt phẳng qua điểm S cách đều các điểm A, B, C, D là
A. 4
B. 2
C. 3
D. 1
Đáp án C
Có 3 mặt phẳng. 2 mặt phẳng là các mặt đi qua điểm S và qua các đường trung trực của AB và AD.1 mặt phẳng qua S và song song với mặt phẳng A B C D .
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD. Số mặt phẳng qua điểm S cách đều các điểm A,B,C,D là:
A. 4
B. 2
C. 3
D. 1
Cho hình chóp tứ giác đều S.ABCD . Số mặt phẳng qua điểm S cách đều các điểm A,B,C,D là:
A. 4
B. 2
C. 3
D. 1
SGK Chân trời sáng tạo
20 tháng 8 2023 lúc 21:50
Cho chóp tứ giác \(S.ABCD\) có đáy là hình chữ nhật với \(AB = 4a,\) \(AD = 3a\). Các cạnh bên đều có độ dài \(5a\). Góc nhị diện \(\left[ {S,BC,A} \right]\) có số đo là
A. \({75^ \circ }46'\).
B. \({71^ \circ }21'\).
C. \({68^ \circ }31'\).
D. \({65^ \circ }12'\).
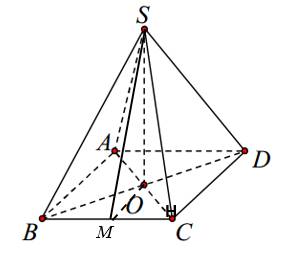
Gọi \(M\) là trung điểm \(BC\).
Ta có:\(OM=\dfrac{1}{2}.AB=2a;AC=\sqrt{AB^2+BC^2}=5a;OC=\dfrac{1}{2}AC=\dfrac{5}{2}a\)
\(SO=\sqrt{SC^2-OC^2}=\dfrac{5\sqrt{3}}{2}a\)
\(\left[S,BC,A\right]=\widehat{SMO}\)
\(\tan\widehat{SMO}=\dfrac{SO}{OM}=\dfrac{5\sqrt{3}}{4}\)
Suy ra:\(\widehat{SMO}=65,2^o\)
\(\Rightarrow D\)
Đúng 1
Bình luận (0)
Cho hình chóp tứ giác đều S. ABCD có tất cả các cạnh đều bằng a. Tính theo a khoảng cách giữa hai đường thẳng AB và SC A.
a
6
2
B.
a
3
3
C.
a
6
3
D. ...
Đọc tiếp
Cho hình chóp tứ giác đều S. ABCD có tất cả các cạnh đều bằng a. Tính theo a khoảng cách giữa hai đường thẳng AB và SC
A. a 6 2
B. a 3 3
C. a 6 3
D. a 3 2
Hình chóp tứ giác đều S.ABCD có các mặt bên là những tam giác đều AB =8cm,O là trung điểm của AC.Độ dài đoạn SO là:
A.82 m
B.6m
C.32 m
D.4m
Kết quả nào đúng?
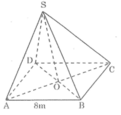
Đáy ABCD là hình vuông nên △ OAB vuông cân tại O.
Áp dụng định lí pi-ta-go ta tính được OA bằng 32
Ta có: SO ⊥ OA nên tam giác AOA cân tại O.
Áp dụng Pi-ta-go vào tam giác vuông SOA ta tỉnh được SO bằng 32
Vậy chọn đáp án C.
Đúng 0
Bình luận (0)