Cho n ∈ ℕ thỏa mãn C n 1 + C n 2 + . . . + C n n = 1023 . Tìm hệ số của x 2 trong khai triển 12 - n x + 1 n thành đa thức.
A. 2
B. 90
C. 45
D. 180
Cho hàm số f n = a n + 1 + b n + 2 + c n + 3 n ∈ ℕ * với a, b, c là hằng số thỏa mãn a + b + c = 0. Khẳng định nào sau đây đúng?
A. l i m x → + ∞ f ( n ) = - 1
B. l i m x → + ∞ f ( n ) = 1
C. l i m x → + ∞ f ( n ) = 0
D. l i m x → + ∞ f ( n ) = 2
Cho dãy số u n thỏa mãn u 1 = 1 u n = 3 u n - 1 + 1 ∀ n ∈ ℕ , n ≥ 2 . Tìm giá trị nhỏ nhất của n để log 9 u n > 100
A. 102
B. 101
C. 202
D. 201
Chọn đáp án D
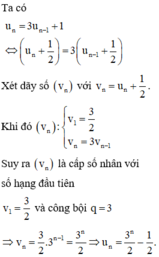
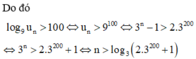
Vậy số tự nhiên n nhỏ nhất thỏa mãn điều kiện trên là n 0 = 201
Cho dãy số u n thỏa mãn u 1 = 2 u n + 1 = u n + 2 − 1 1 − 2 − 1 u n , ∀ n ∈ ℕ * Tính u 2018 .
A. u 2018 = 7 + 5 2
B. u 2018 = 2
C. u 2018 = 7 − 5 2
D. u 2018 = 7 + 2
Đáp án A
Đặt u 1 = tan α ⇒ u 2 = tan α + tan π 8 1 − tan α . tan π 8 = tan α + π 8 .
Tương tự dung quy nạp suy ra:
u n = tan α + π n − 1 8 ⇒ u 2018 = tan α + 2017 π 8 = tan α + π 8 = u 2 = 7 + 5 2 .
Cho dãy số un thỏa mãn u 1 = 2 u n + 1 = u n + 2 − 1 1 − 2 − 1 u n , ∀ n ∈ ℕ ∗ . Tính u 2018 .
A. u 2018 = 7 + 5 2
B. u 2018 = 2
C. u 2018 = 7 − 5 2
D. u 2018 = 7 + 2
Đáp án A
Ta có tan π 8 = 2 − 1 suy ra u n + 1 = u n + tan π 8 1 − tan π 8 . u n
Đặt tan φ = 2 suy ra u 1 = tan φ → u 2 = u 1 + tan π 8 1 − tan π 8 . u 1 = tan φ + tan π 8 1 − tan φ . tan π 8 = tan φ + π 8
Do đó u 3 tan φ + 2. π 8 → u n tan φ + n . π 8
Vậy u 2018 = tan φ + 2017. π 8 = tan φ + π 8 = u 2 = 2 + 2 − 1 1 − 2 2 − 1 = 7 + 5 2
Cho n ∈ ℕ thỏa mãn nC1+nC2+...+nCn=1023. Tìm hệ số của x2 trong khai triển [ ( 12 - n ) x + 1 ] n thành đa thức
A.2.
B.90.
C.45.
D.180.
Cho khai triển nhị thức Niuton x 2 + 2 n x n với n n ∈ ℕ , x > 0. Biết rằng số
hạng thứ 2 của khai triển bằng 98 và n thỏa mãn A n 2 + 6 C n 3 = 36 n Trong các giá trị x sau, giá trị nào thỏa mãn?
A. 3
B. 4
C. 1
D. 2
Cho dãy số u n thỏa mãn log u 1 2 + u 2 2 + 10 - log 2 u 1 + 6 u 2 = 0 v à u n + 2 + u n = 2 u n + 1 + 1 với mọi n ∈ ℕ * . Giá trị nhỏ nhất của n để u n > 5050 bằng
A. 101
B. 102
C. 100
D. 99
Cho n ∈ ℕ ; n > 3 thỏa mãn phương trình
log 4 n - 3 + log 4 n + 9 = 3
Tổng phần thực và phần ảo của số phức z = 1 + i n
A. 3
B. 2
C. 1
D. 0
Ta có
log 4 n - 3 + log 4 n + 9 = 3 ⇔ log 4 n - 3 n + 9 = 3 ⇔ n 2 + 6 b - 91 = 0 ⇔ n = n = - 13 z = 1 + i 7 = 1 + i 1 + i 2 3 = 8 - 8 i
Vậy tổng phần thực và phần ảo của số phức z bằng 0
Đáp án D
Tìm giá trị n ∈ ℕ thỏa mãn A n 2 - C n + 1 n - 1 = 5
A. n = 3
B. n = 5
C. n = 4
D. n = 6
Cho f n = n 2 + n + 1 2 + 1 ∀ n ∈ ℕ ∗ . Đặt u n = f 1 . f 3 ... f 2 n − 1 f 2 . f 4 ... f 2 n .
Tìm số n nguyên dương nhỏ nhất sao cho u n thỏa mãn điều kiện log 2 u n + u n < − 10239 1024 .
A. n = 23
B. n = 29
C. n = 21
D. n = 33
Đáp án A
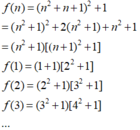
= > U n = ( 1 2 + 1 ) ( 2 2 + 1 ) . ( 3 2 + 1 ) ( 4 2 + 1 ) ... [ ( 2 n − 1 ) 2 + 1 ] [ ( 2 n ) 2 + 1 ] ( 2 2 + 1 ) ( 3 2 + 1 ) . ( 4 2 + 1 ) ( 5 2 + 1 ) ... [( 2 n ) 2 + 1 ] [ ( 2 n + 1 ) 2 + 1 ] = > U n = 2 ( 2 n + 1 ) 2 + 1
