Một hình trụ có bán kính đáy a 3 , chiều cao là 2 a 3 . Diện tích của mặt cầu nội tiếp hình trụ bằng:
A. 4 3 πa 3
B. 24 πa 2
C. 8 6 πa 2
D. 12 πa 2
Một hình trụ có bán kính đáy a 3 , chiều cao là 2 a 3 . Diện tích của mặt cầu nội tiếp hình trụ bằng:
A . 4 3 πa 3
B . 24 πa 2
C . 8 3 πa 2
D . 12 πa 2
Đáp án D.
Vì khối cầu nội tiếp khối trụ nên khối cầu có bán kính là nên diện tích của mặt cầu ![]()
Một hình trụ có bán kính đáy a 3 , chiều cao là 2 a 3 . Diện tích của mặt cầu nội tiếp hình trụ bằng
A. 4 3 π a 3
B. 24 π a 2
C. 8 6 π a 2
D. 12 π a 2
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
A. h = R 2
B. h = R
C. h = R 2
D. h = R 2 2
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
A. h = R 2 .
B. h = R
C. h = R 2 .
D. h = R 2 2 .
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
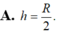
![]()
![]()
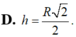
Cho mặt cầu (S) bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất
A. h = R 2
B. h = R 2
C. h = R 2 2
D. h = R
Đáp án A
Vì hình trụ nội tiếp trong mặt cầu bán kính R cố định
⇒ R 2 = r 2 + h 2 2 = r 2 + h 2 4 ≥ 2 r 2 × h 2 4 = r h ⇒ r h = R 2
Diện tích xung quanh của hình trụ là: S x q = 2 πrh ≤ 2 πR 2
Dấu “=” xảy ra khi r 2 + h 2 4 = R 2 r 2 = h 2 4 ⇒ h = R 2 .
Chiều cao của một hình trụ gấp 3 lần bán kính đáy của nó.Tỉ số thể tích của hình trụ này và thể tích của hình cầu có bán kính bằng bán kính đáy của hình trụ là:
A. 4 3 B. 9 4
C. 3 1 D. 4 9
Thể tích hình trụ : V 1 = πr 2 h = πr 2 .3r = 3 πr 3 (đvdt)
Thể tích hình cầu : V 2 = (4/3). πr 3 (đvdt)
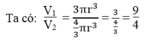
Vậy chọn đáp án B
Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r và có trục là OO'
a) Chứng minh rằng mặt cầu đường kính OO' tiếp xúc với hai mặt đáy của hình trụ và tiếp xúc với tất cả các đường sinh của mặt trụ
b) Cắt hình trụ bởi một mặt phẳng song song với trục OO' và cách trục một khoảng bằng \(\dfrac{r}{2}\). Tính diện tích thiết diện thu được
c) Thiết diện nói trên cắt mặt cầu đường kính OO' theo thiết diện là một đường tròn. Tính bán kính của đường tròn đó
Cho hình trụ có chiều cao h = a 5 bán kính đáy r = a . Tính diện tích S của mặt cầu ngoại tiếp hình trụ đã cho.
A. S = 9 π a 2
B. S = 32 π a 2
C. S = 24 π a 2
D. S = 3 π a 2