Cho n ∈ ℕ ; n > 3 thỏa mãn phương trình
log 4 n - 3 + log 4 n + 9 = 3
Tổng phần thực và phần ảo của số phức z = 1 + i n
A. 3
B. 2
C. 1
D. 0
Những số nào sau đây chia cho 8 dư 1?
8.n (với n ∈ ℕ)
8.n + 1 (với n ∈ ℕ)
8.n - 1 (với n ∈ ℕ*)
8.(n + 1) (với n ∈ ℕ)
8.(n + 1) + 1 (với n ∈ ℕ)
Số chia 8 dư 1 có dạng 8x + 1 (với x thuộc N)
Xét từng đáp án:
8n \(⋮\)8 (loại) (n thuộc N)
8n + 1 (chọn) (...)
8n - 1 = 8n + 8 - 7 = 8.(n + 1) - 7 chia 8 dư 7 (loại) (...)
8.(n + 1) \(⋮\)8 (loại) (...)
8.(n + 1) + 1 chia 8 dư 1 (chọn) (...)
Vì 8.(n + 1) \(⋮\)8 và 1 chia 8 dư 1
Vậy có 8n + 1 và 8.(n + 1) + 1 thỏa mãn đề bài
Những số nào sau đây chia cho 6 dư 3?
6.n (với n ∈ ℕ)
6.n + 3 (với n ∈ ℕ)
6.n - 3 (với n ∈ ℕ*)
6.(n + 3) (với n ∈ ℕ)
6.(n + 3) + 3 (với n ∈ ℕ)
xời dăm ba cái bài này tui...........................ko thik làm
+ Ta có: \(6n⋮6\forall n\)\(\Rightarrow\)\(6n+3:6\)dư \(3\)
\(6n-3:6\)dư \(6-3=3\)
+ Ta lại có: \(6.\left(n+3\right)⋮6\forall n\)\(\Rightarrow\)\(6.\left(n+3\right)+3:6\)dư \(3\)
Vậy \(6n+3,\)\(6n-3,\)\(6.\left(n+3\right)+3\)chia 6 dư 3
6.n + 3 (với n ∈ ℕ) ( vì \(6n⋮6\), 3 không chia hết cho 6 )
6.n - 3 (với n ∈ ℕ ) ( vì \(6n⋮6\), 3 không chia hết cho 6 )
6.(n + 3) + 3 (với n ∈ ℕ) ( vì \(6\left(n+3\right)⋮6\), 3 không chia hết cho 6 )
\(\rightarrow\)Chia 6 dư 3
Cho các tập hợp: A = { m ∈ ℕ | m là ước của 16} } ; B = { n ∈ ℕ | n là ước của 24}. Tập hợp A ∩ B là:
A. ∅
B. { 1 ; 2 ; 4 ; 8 }
C. { ± 1 ; ± 2 ; ± 4 ; ± 8 }
D. { 1 ; 2 ; 4 ; 8 ; 16 }
Cho hai tập hợp A = { a = 3 n | n ∈ ℕ * } , B = { b ∈ ℕ | 0 < b ≤ 9 } .
Khẳng định nào dưới đây là không đúng?
A. A ∩ B = { 3 ; 6 ; 9 }
B. B ⊂ A
C. 15 ∈ A ,15 ∉ B
D. 18 ∈ A ,9 ∈ A ,9 ∈ B
Ta có A = a = 3 n | n ∈ N * = 3 ; 6 ; 9 ; 12 ; ...
B = b ∈ N | 0 < b ≤ 9 = 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9
Ta thấy; 2 ∈ B ; 2 ∉ A nên B không thể là tập con của A.
Khẳng định B sai.
Đáp án B
Cho k ∈ ℕ , n ∈ ℕ . Trong các công thức về số các chỉnh hợp và số các tổ hợp sau, công thức nào là công thức đúng?
A. C n k = n ! ( n - k ) ! với 0 ≤ k ≤ n
B. A n k = n ! k ! ( n - k ) ! với 0 ≤ k ≤ n
C. C n + 1 k = C n k + C n k - 1 với 1 ≤ k ≤ n
D. C n + 1 k = C n k + 1 với 0 ≤ k ≤ n - 1
Cho k ∈ ℕ , n ∈ ℕ . Trong các công thức về số các chỉnh hợp và số các tổ hợp sau, công thức nào là công thức đúng?
A. C n k = n ! n − k ! 0 ≤ k ≤ n
B. A n k = n ! k ! n − k ! 0 ≤ k ≤ n
C. C n + 1 k = C n k + C n k − 1 1 ≤ k ≤ n
D. C n + 1 k = C n k + 1 0 ≤ k ≤ n − 1
Đáp án C
Công thức tính số chỉnh hợp chập k của n: A n k = n ! n − k ! .
Công thức tính số tổ hợp chập k của n : C n k = n ! k ! n − k ! .
Hai tính chất cơ bản của tổ hợp: C n k = C n n − k
C n + 1 k = C n k + C n k − 1
Quan sát các đáp án đã cho ta thấy đáp án C đúng.
Số phần tử của tập A = ( − 1 ) 2 n + 1 , n ∈ ℕ * A = ( − 1 ) 2 n + 1 , n ∈ ℕ * là:
A. 3
B. 1
C. Vô số
D. 2
Đáp án A
Ta có: ( − 1 ) 2 n + 1 = − 1 , ∀ n ∈ ℕ * nên A = {-1}
Vậy A chỉ có 1 phần tử
Tìm n ∈ \(ℕ\), n ≥ 1 sao cho tổng 1! + 2! + 3! + ... + n! là 1 số chính phương
Xét các trường hợp:
\(n=1\Leftrightarrow1!=1=1^2\) là số chính phương
\(n=2\Leftrightarrow1!+2!=3\) không phải là số chính phương
\(n=3\Leftrightarrow1!+2!+3!=9=3^3\) là số chính phương
\(n\ge4\Leftrightarrow1!+2!+3!+4!=33\) còn \(5!,6!,7!,...,n!\) đều có tận cùng là \(0\Rightarrow1!+2!+3!+...+n!\) có tận cùng là chữ số 3 nên không phải là số chính phương
Vậy \(n\in\left\{1;3\right\}\).
Cho các khẳng định sau:
(I) ℕ ∩ ℤ = ℕ
(II) ℝ \ ℚ = ℤ
(III) ℚ ∪ ℝ = ℝ
(IV) ℚ ∪ ℕ * = ℕ *
Trong các khẳng định trên, có bao nhiêu khẳng định là mệnh đề đúng?
A. 1
B. 2
C. 3
D. 4
Các khẳng định đúng là (I), (III)
Đáp án B
Cho n ∈ ℕ * ; C n - 2 2 + C n 8 C n n - 8 = 2 C n 2 C n n - 8 . Tính T = 1 2 C n 1 + 2 2 C n 2 + . . . . + n 2 C n n ?
A . 55 . 2 9
B . 55 . 2 10
C . 5 . 2 10
D . 55 . 2 8
Chọn A
Ta có ![]()
![]()
![]()
![]()
![]()
![]()
Ta có ![]()
![]()
Đạo hàm hai vế ta được: ![]()
![]()
![]()
![]()
Đạo hàm 2 vế ta được: 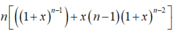
![]()
Thay x = 1 vào 2 vế : ![]()
![]()
Với n = 10, T =
1
2
C
n
1
+
2
2
C
n
2
+
.
.
.
.
+
n
2
C
n
n
![]()
![]()
![]()