Cho hình chóp S.ABCD đáy ABCD là hình bình hành AB = a, AC = a 2 , B C = a 3 2 , ∆ SAD vuông cân tại S và (SAD) ⊥ (ABCD). Tính thể tích V của SABCD.
A. V = a 3 16
B. V = a 3 3 24
C. V = a 3 6 2
D. V = a 3 6 6
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình bình hành có AB ⊥ AC. Biết SA = AD = a. Tính khoảng cách h từ A tới mặt phẳng (SCD).
A. h = a 2 2
B. h = a 3 7
C. h = a 3 2
D. h = a 2
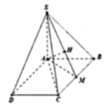
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD tâm O tam giác ABC vuông cân tại A, có AB = AC = a, S A ⊥ ( A B C D ) . Đường thẳng SD tạo với đáy một góc 45 o . Khoảng cách giữa 2 đường thẳng AD và SB là?
A. a 3 2
B. a 5 5
C. a 10 10
D. a 10 5
Đáp án: D.
Hướng dẫn giải:
Lấy M là trung điểm BC, H là hình chiếu của A lên SM. Xác định
![]()
S A ⊥ B C ⊥ A M
![]()
⇒ A H ⊥ S M ⇒ A H ⊥ ( S B C )
⇒ d ( A , ( S B C ) ) = A H
Vì AD//(SBC) chứa BC nên
d(SB,AD)=d(AD,(ABC))=d(A,(SBC))=AH
Tính: SA=AD= a 2 ,AM= a 2
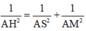
⇒ A H = a 2 5
Bài 3 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M, N là trung điểm cạnh SC; SD
a) CMR: MN // (SAB); MM // (ABCD)
b) CMR: MO // (SAB)
Bài 4 :Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M,N, P là trung điểm cạnh SA, SB, SC.
a) Chứng minh rằng : MN // (SCD).
b) Chứng minh rằng: MO // (SAB)
Giúp vs bạn !!
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , A C = a 3 , B C = 2 a . Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Chiều cao SH của hình chóp là
A. a 15 5
B. a 15 3
C. 2 a 15
D. a 5 3
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , A C = a 3 , B C = 2 a . Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Chiều cao SH của hình chóp là
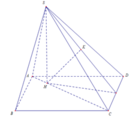
A. a 15 5
B. a 15 3
C. 2 a 15
D. a 5 3
Đáp án C
![]()
![]()
![]()
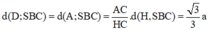
⇔ d ( H ; S B C ) = H K
1 S H 2 + 1 H M 2 = 1 H K 2
⇒ S H = 2 15 a
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , A C = a 3 , B C = 2 a . Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Chiều cao SH của hình chóp là
A. a 15 5
B. a 15 3
C. 2 a 15
D. a 5 3
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt S A → = a → , S B → = b → , S C → = c → , S D → = d → . Chứng minh: a → + c → = d → + b → .
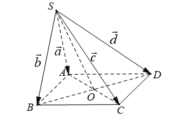
- Gọi O là tâm của hình bình hành ABCD. Ta có:
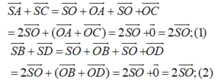
- Từ (1) và (2) suy ra:
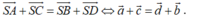
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AB = a, SA = a 3 vuông góc với (ABCD). Tính góc giữa hai đường thẳng SB và CD.
A. 60 °
B. 30 °
C. 45 °
D. 90 °
Chọn A.
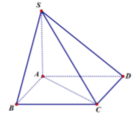
Ta có ABCD là hình bình hành => AB//CD
Do đó (SB,CD) = (SB,AB) = SBA
Vì SA ⊥ (ABCD) => SA ⊥ AB => ∆ SAB vuông tại A.
Xét tam giác vuông SAB ta có: ![]()
Vậy (SB;CD) = 60 °
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , S A = a 3 và S A ⊥ A B C D . Tính góc giữa hai đường thẳng SB và CD
A. 600.
B. 300.
C. 450.
D. 900.
Chọn đáp án A
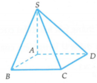
Ta có ABCD là hình bình hành nên CD//AB.
Lại có S A ⊥ A B C D ⇒ S A ⊥ A B
⇒ ∆ S A B vuông tại A.
Suy ra
![]()
Trong tam giác SAB vuông tại A có
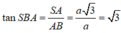
⇒ S B A ⏜ = 60 0