Tìm giá trị của tham số m để phương trình sin x − 1 cos 2 x − cos x + m = 0 có đúng 5 nghiệm thuộc đoạn 0 ; 2 π
A. 0 ≤ m < 1 4
B. − 1 4 < m ≤ 0
C. 0 < m < 1 4
D. − 1 4 < m < 0
Những câu hỏi liên quan
Có bao nhiêu giá trị nguyên của tham số m để phương trình
1
+
2
cos
x
+
1
+
2
sin
x
...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình 1 + 2 cos x + 1 + 2 sin x = 1 2 m có nghiệm?
A. 3.
B. 5.
C. 4.
D. 2.
Câu 1 : Giá trị lớn nhất của biểu thức P= 3 sin x +4 cosx là
Câu 2: Tính giá trị của biểu thức P=(sin²x-1)tan²x+ (cos²x-1)cot²x
Câu 3: Tìm các giá trị của tham số m để phương trình (x-2)(x-2mx+1)=0 có 2 nghiệm phân biệt
Xem chi tiết
Có bao nhiêu giá trị nguyên của tham số m để phương trình
sin
2
x
+
cos
2
x
+
|
sin
x
+
cos
x
|
-
cos
2
x
+
m
-
m
0
có nghiệm thực? A. 9 B. 2 C. 3 D. 5
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình sin 2 x + cos 2 x + | sin x + cos x | - cos 2 x + m - m = 0 có nghiệm thực?
A. 9
B. 2
C. 3
D. 5
Đáp án C
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
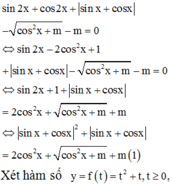
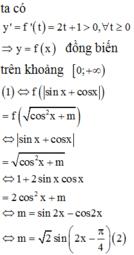
Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
Đúng 0
Bình luận (0)
Số giá trị nguyên của m để phương trình \(2\sin^2x-\sin x\cos x-m\cos^2x=1\) có nghiệm trên
Cho phương trình m. sin x + 4. cos x = 2m - 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm?
A. 4
B. 7.
C. 6.
D. 5
11 tháng 10 2021 lúc 7:14
Để phương trình:
\(2^{sin\left(x\right)^2}+2^{cos\left(x\right)^2}=m\) có nghiệm, thì các giá trị cần tìm của tham số m là
Bài này có cách nào bấm máy không vậy ạ ??
giúp em câu này với ạ ;-;câu 1: tìm tất cả các giá trị của tham số m để phương trình dfrac{x}{sqrt{1-x^2}}dfrac{5-2m}{sqrt{1-x^2}} có nghiệmcâu 2: cho tanαdfrac{-2}{3}. Khi đó biểu thức M dfrac{sinalpha.cosalpha}{sin^2alpha-cos^2alpha}có giá trị bằng bao nhiêu ?em cảm ơn nhiều nhiều lắm luônnn :
Đọc tiếp
giúp em câu này với ạ ;-;
câu 1: tìm tất cả các giá trị của tham số m để phương trình \(\dfrac{x}{\sqrt{1-x^2}}=\dfrac{5-2m}{\sqrt{1-x^2}}\) có nghiệm
câu 2: cho tanα=\(\dfrac{-2}{3}\). Khi đó biểu thức M = \(\dfrac{sin\alpha.cos\alpha}{sin^2\alpha-cos^2\alpha}\)có giá trị bằng bao nhiêu ?
em cảm ơn nhiều nhiều lắm luônnn :>>
1.
ĐKXĐ: \(1-x^2>0\Leftrightarrow0< x< 1\)
Pt tương đương:
\(x=5-2m\)
Pt có nghiệm khi và chỉ khi:
\(0< 5-2m< 1\) \(\Leftrightarrow2< m< \dfrac{5}{2}\)
2.
\(M=\dfrac{\dfrac{sina.cosa}{cos^2a}}{\dfrac{sin^2a}{cos^2a}-\dfrac{cos^2a}{cos^2a}}=\dfrac{tana}{tan^2a-1}=\dfrac{\left(-\dfrac{2}{3}\right)}{\left(-\dfrac{2}{3}\right)^2-1}=-\dfrac{6}{5}\)
Đúng 1
Bình luận (0)
Số giá trị nguyên của tham số m thuộc đoạn
-
2018
,
2018
để phương trình
m
+
1
.
sin
2
x
-
sin
2
x
+
cos
...
Đọc tiếp
Số giá trị nguyên của tham số m thuộc đoạn - 2018 , 2018 để phương trình m + 1 . sin 2 x - sin 2 x + cos 2 x = 0 có nghiệm là:
A. 4037
B. 4036
C. 2019
D. 2020
Phương trình
15
.
sin
x
+
cos
x
m
với m là tham số có nghiệm khi giá trị của m bằng
Đọc tiếp
Phương trình 15 . sin x + cos x = m với m là tham số có nghiệm khi giá trị của m bằng
Tìm tất cả các giá trị thực của tham số m để phương trình
2
.
sin
2
x
-
(
2
m
+
1
)
.
sin
x
+
2
m
-
1
0
có nghiệm thuộc khoảng
-
π...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 2 . sin 2 x - ( 2 m + 1 ) . sin x + 2 m - 1 = 0 có nghiệm thuộc khoảng - π 2 , 0 .
