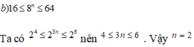Tìm số nguyên dương n, biết:16 ≤ 8n ≤ 64.

Những câu hỏi liên quan
Tìm số nguyên dương n biết: 16 ≤ 8 n ≤ 64
tìm số nguyên dương n, biết:
a) 25<5n<625
b)3.27>3nlớn hơn, bằng 9
c)16 bé hơn, bằng 8n bé hơn, bằng 64
a) \(25< 5^n< 625\)
\(25=5^2;625=5^4\)
=> \(5^2< 5^n< 5^4\)
=> 2 < n < 4
=> n = 3
b) \(9\le3^n< 3.27\)
\(9=3^2;3.27=3.3^3=3^4\)
=> \(3^2\le3^n< 3^4\)
=> n = 2; hoặc n = 3
c) \(16\le8^n\le64\)
\(16=8.2;64=8^2\)
=> \(8.2\le8^n\le8^2\)
=> n = 2
Tìm số tự nhiên n biết:
\(C=\frac{n^4-1}{n^4-4n^3+8n^2+16}\) có giá trị là một số nguyên
Tìm các số nguyên n thỏa mãn n4 + 8n + 11 có thể viết thành tích của hai hay nhiều số nguyên dương liên tiếp.
Cho dãy số
u
n
thỏa mãn
log
3
2
u
5
-
63
2
log
4
u
n
-
8
n
+
8...
Đọc tiếp
Cho dãy số u n thỏa mãn log 3 2 u 5 - 63 = 2 log 4 u n - 8 n + 8 , ∀ n ∈ N * . Đặt S n = u 1 + u 2 + . . . + u n . Tìm số nguyên dương lớn nhất n thỏa mãn u n . S 2 n u 2 n . S n < 148 75
A. 18
B. 17
C. 16
D. 19
Tìm các số n nguyên dương sao cho \(\left(n^3-8n^2+2n\right)⋮\left(n^2+1\right)\)
Tìm n là số nguyên dương biết 5^3n.5^3n+5.5^4n < hoặc=10^16:2^16
Tìm số nguyên dương n để phân số 9n-51/8n-53 đạt giá trị lớn nhất. tính giá trị lớn nhất đó ?
Lời giải:
\(\frac{9n-51}{8n-53}=\frac{\frac{9}{8}(8n-53)+\frac{69}{8}}{8n-53}\\
=\frac{9}{8}+\frac{69}{8(8n-53)}\)
Để phân số trên max thì $\frac{69}{8(8n-53)}$ max.
Điều này xảy ra khi $8n-53$ là số dương nhỏ nhất
$\Rightarrow n$ phải là số nguyên dương nhỏ nhất để $8n-53$ là số dương nhỏ nhất.
$8n-53>0\Rightarrow n> 6,625$
$\Rightarrow$ số nguyên dương $n$ nhỏ nhất thỏa mãn là $7$.
Đúng 0
Bình luận (0)
Chứng tỏ 8n+2-5n+2+8n-5n chia hết cho 65 và 120 với mọi số n nguyên dương
Ta có: \(8^{n+2}+8^n-5^{n+2}-5^n\)
\(=8^n\left(64+1\right)-5^n\left(5^2+1\right)\)
\(=8^n\cdot65-5^{n-1}\cdot130⋮65\)
Đúng 0
Bình luận (0)