Trong không gian Oxyz, cho 2 véc tơ u → = ( 1 ; a ; 2 ) , v → = ( - 3 ; 9 ; b ) cùng phương. Tính a 2 + b .
A. 15.
B. 3.
C. 0 .
D. Không tính được.
Trong không gian với hệ tọa độ Oxyz, cho véc-tơ ![]() =(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ
=(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ ![]() ?
?
![]()
![]()
![]()
![]()
Trong không gian Oxyz, véc tơ nào dưới đây vuông góc với cả hai véc tơ u → = ( - 1 ; 0 ; 2 ) , v → = ( 4 ; 0 ; - 1 ) ?
A. w → =(0;7;1)
B. w → =(1;7;1)
C. w → =(0;-1;0)
D. w → =(-1;7-1)
#2H3Y1-1~Trong không gian Oxyz, cho véc-tơ ![]() sao cho
sao cho ![]() . Tọa độ của véc-tơ
. Tọa độ của véc-tơ ![]() là:
là:
A. (-2;1;2)
B. (1;2;-2)
C. (2;1-2)
D. (2;1;2).
Trong không gian Oxyz, cho 2 véc tơ a → ( 1 ; - 5 ; 2 ) , b → ( 2 ; - 4 ; 0 ) Tính tích vô hướng của 2 véc tơ a → và b → .
A. a → . b → = - 22
B. a → . b → = 22
C. a → . b → = 11
D. a → . b → = - 11
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 1 2 = y - 2 1 = z + 1 2 nhận véc tơ u ⇀ ( a ; 2 ; b ) làm véc tơ chỉ phương. Tính a+b
A. -8
B. 8
C. 4
D. -4
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 1 2 = y - 2 1 = z + 1 2 nhận véc tơ u → = a ; 2 ; b làm véc tơ chỉ phương. Tính a + b
A. - 8
B. 8
C. 4
D. - 4
Trong không gian tọa độ Oxyz, cho đường thẳng d : x - 1 1 = y - 1 - 1 = z - 1 1 Véc tơ nào trong các véc tơ sau đây không là véc tơ chỉ phương của đường thẳng d?
A. u 1 → =(-2;2;-2)
B. u 1 → =(-3;3;-3)
C. u 1 → =(2;-4;4)
D. u 1 → =(1;1;1)
Đáp án D
Phương pháp:
Đường thẳng
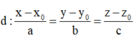
có 1 VTCP là u 1 → =(a;b;c). Mọi vectơ v → =k u → (k ∈ Z)cùng phương với vecto u → đều là VTCP của đường thẳng d.
Cách giải: Đường thẳng d nhận u → =(1;-1;1) là 1 VTCP. Mọi vecto cùng phương với vecto đều là VTCP của đường thẳng d.
Ta thấychỉ có đáp án D, vecto u 1 → =(1;1;1) không cùng phương với u → =(1;-1;1) nên u 1 → =(1;1;1) không là VTCP của đường thẳng d.
Trong không gian Oxyz, cho ba véc tơ a → ( 5 ; 7 ; 2 ) , b → ( 3 ; 0 ; 4 ) , c → ( - 6 ; 1 ; - 1 ) . Hãy tìm véc tơ n → = 3 a → - 2 b → + c →
A. (3; 22; -3)
B. (-3; 22; 3)
C. (3; -22; 3)
D. (3; -22; -3)
Trong không gian tọa độ Oxyz, cho đường thẳng d: ![]() .Véc tơ nào trong các véc tơ sau đây không là véc tơ chỉ phương của đường thẳng d?
.Véc tơ nào trong các véc tơ sau đây không là véc tơ chỉ phương của đường thẳng d?
A. u 1 → = 2 ; - 2 ; 2
B. u 1 → = - 3 ; 3 ; - 3
C. u 1 → = 4 ; - 4 ; 4
D. u 1 → = 1 ; 1 ; 1
Đáp án D
Phương pháp:
Đường thẳng d: 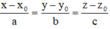 có 1 VTCP là
có 1 VTCP là ![]() . Mọi vectơ
v
→
=
k
u
→
(
k
∈
Z
)
cùng phương với vecto
u
→
đều là VTCP của đường thẳng d
. Mọi vectơ
v
→
=
k
u
→
(
k
∈
Z
)
cùng phương với vecto
u
→
đều là VTCP của đường thẳng d
Cách giải: Đường thẳng d nhận u 1 → = 1 ; - 1 ; 1 là 1 VTCP. Mọi vecto cùng phương với vecto đều u → là VTCP của đường thẳng d.
Ta thấy chỉ có đáp án D, vecto u 1 → = 1 ; 1 ; 1 không cùng phương với u 1 → = 1 ; - 1 ; 1 nên u 1 → = 1 ; 1 ; 1 không là VTCP của đường thẳng d