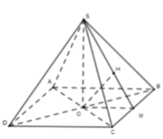
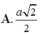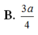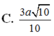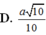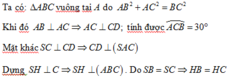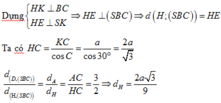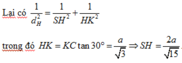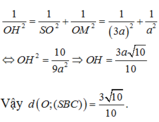cho hình chóp tứ giác ddeuf S.ABCD,có cạnh đáy bằng a.SH là đường cao.khoảng cách từ trung điểm I của SH đén mặt (SBC) bằng b.Tính thể tích khối chóp SABCD theo a và b
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AD a, AB 2a, BC 3a, SA 2a. H là trung điểm cạnh AB, SH là đường cao của hình chóp S.ABCD, Tính khoảng cách từ điểm A đến mp (SCD)
A
.
a
30
7
B
.
a
30
10
C
.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AD = a, AB = 2a, BC = 3a, SA = 2a. H là trung điểm cạnh AB, SH là đường cao của hình chóp S.ABCD, Tính khoảng cách từ điểm A đến mp (SCD)
A . a 30 7
B . a 30 10
C . a 13 10
D . a 13 7
Đáp án B
Gọi H 1 là chân đường cao kẻ từ H đến DC. H 2 là chân đường cao kẻ từ H đến S H 1 . Khi đó ta có
![]()
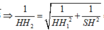
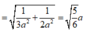
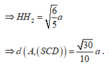
=> Chọn phương án B.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành,
A
B
a
,
A
C
a
3
,
B
C
2
a
. Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng
a
3
3
. Chiều cao SH của hình chóp là A. ...
Đọc tiếp
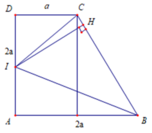
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , A C = a 3 , B C = 2 a . Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Chiều cao SH của hình chóp là
A. a 15 5
B. a 15 3
C. 2 a 15
D. a 5 3
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành,
A
B
a
,
A
C
a
3
,
B
C
2
a
. Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằn...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , A C = a 3 , B C = 2 a . Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Chiều cao SH của hình chóp là
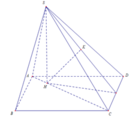
A. a 15 5
B. a 15 3
C. 2 a 15
D. a 5 3
Đáp án C
![]()
![]()
![]()
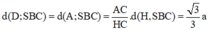
⇔ d ( H ; S B C ) = H K
1 S H 2 + 1 H M 2 = 1 H K 2
⇒ S H = 2 15 a
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành,
A
B
a
,
A
C
a
3
,
B
C
2
a
.
Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng
a
3
3
. Chiều cao SH của hìn...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , A C = a 3 , B C = 2 a . Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Chiều cao SH của hình chóp là
A. a 15 5
B. a 15 3
C. 2 a 15
D. a 5 3
Cho hình chóp tứ giác đều S.ABCD có đường cao SH 6cm, cạnh đáy bằng 6cm. Lấy điểm H’ SH sao cho SH’
2
3
. Một mặt phẳng đi qua H’ và song song với đáy và cắt mặt bên của hình chóp tạo thành hình chóp nhỏ S.A’B’C’D’ và hình chóp cụt ABCD.A’B’C’D’. Tính thể tích của hình chóp S.ABCD. A. 32
c
m
3
B. 72
c
m
3
C. 16
c...
Đọc tiếp
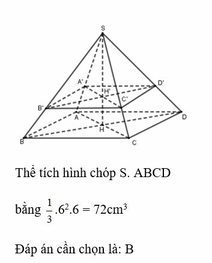
Cho hình chóp tứ giác đều S.ABCD có đường cao SH = 6cm, cạnh đáy bằng 6cm. Lấy điểm H’ SH sao cho SH’ = 2 3 . Một mặt phẳng đi qua H’ và song song với đáy và cắt mặt bên của hình chóp tạo thành hình chóp nhỏ S.A’B’C’D’ và hình chóp cụt ABCD.A’B’C’D’. Tính thể tích của hình chóp S.ABCD.
A. 32 c m 3
B. 72 c m 3
C. 16 c m 3
D. 64 c m 3
Cho hình chóp tứ giác đều S.ABCD có đường cao SH 6cm, cạnh đáy bằng 4cm. Một mặt phẳng đi qua trung d diểm H’ của SH và song song với đáy và cắt mặt bên của hình chóp tạo thành hình chóp nhỏ S.A’B’C’D’ và hình chóp cụt. Tính thể tích của hình chóp S.ABCD A. 32
c
m
3
B. 31
c
m
3
C. 16
c
m
3
D. 64
c...
Đọc tiếp
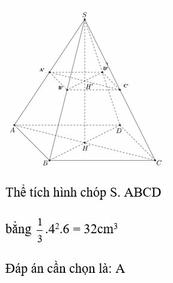
Cho hình chóp tứ giác đều S.ABCD có đường cao SH = 6cm, cạnh đáy bằng 4cm. Một mặt phẳng đi qua trung d diểm H’ của SH và song song với đáy và cắt mặt bên của hình chóp tạo thành hình chóp nhỏ S.A’B’C’D’ và hình chóp cụt. Tính thể tích của hình chóp S.ABCD
A. 32 c m 3
B. 31 c m 3
C. 16 c m 3
D. 64 c m 3
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và khoảng cách từ A đến (SBC) bằng
a
6
3
. Thể tích của hình chóp bằng:A.
6
24
a
3
B.
2
9
a...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và khoảng cách từ A đến (SBC) bằng a 6 3 . Thể tích của hình chóp bằng:
A. 6 24 a 3 B. 2 9 a 3
C. 2 8 a 3 D. 2 6 a 3
Chọn D.
Gọi H, M, N theo thứ tự là các trung điểm của các cạnh AC, BC, AD.
Kẻ NI ⊥ SM (I ∈ SM). Để ý rằng AN // (SBC)
Do đó NI = d(N,(SBC)) = d(A,(SBC)) = a 6 3
Từ hai tam giác đồng dạng SHM và NIM ta tính được SH.
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O cạnh 2a. Thể tích khối chóp S.ABCD bằng
4
a
3
.
Tính khoảng cách từ điểm O tới mặt bên của hình chóp. A.
a
2
2
B.
3
a
4
C.
3
a
10...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O cạnh 2a. Thể tích khối chóp S.ABCD bằng 4 a 3 . Tính khoảng cách từ điểm O tới mặt bên của hình chóp.
A. a 2 2
B. 3 a 4
C. 3 a 10 10
D. a 10 10
Chọn C.
Phương pháp
Sử dụng quan hệ vuông góc giữa đường thẳng và mặt phẳng để xác định khoảng cách

Ta tính SO dựa vào công thức thể tích hình chóp, tính OH dựa vào hệ thức lượng trong tam giác vuông.
Cách giải:
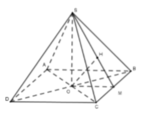


Xét tam giác SOM vuông tại M có OH là đường cao nên theo hệ thức lượng trong tam giác vuông ta có
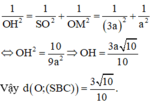
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O cạnh 2a. Thể tích khối chóp S.ABCD bằng
4
a
3
. Tính khoảng cách từ điểm O tới mặt bên của hình chóp.
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O cạnh 2a. Thể tích khối chóp S.ABCD bằng 4 a 3 . Tính khoảng cách từ điểm O tới mặt bên của hình chóp.