Tích phân ∫ 0 1 d x 2 x + 5 bằng
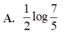

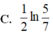
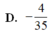
1.Phân tích đa thức thành nhân tử
a, x^3z+x^2yz-x^2z^2-xyz^2
b, x^3+x^2y-x^2z-xyz
c, a^2x+a^2y+ax+ay+x+y
d, xa+xb+ya+yb-za-zb
2.Phân tích đa thức thành nhân tử
a, a^2+2ab+b^2-c^2+2cd-d^2
b, x^2-4xy+4y^2-x+2y
c,2^2-(x-1)^2+2(x-1)-1
d, xz-yz-x^2+2xy-y^2
3.Tìm x biết
a, x(2x-7)-4x+14 = 0
b, x(x-1)+2x-2 = 0
c, x+x^2-x^2-x^4 = 6
d, 2x^3+3x^2+2x+3 =0
Bài 3:
a: =>(2x-7)(x-2)=0
=>x=7/2 hoặc x=2
b: =>(x-1)(x+2)=0
=>x=1 hoặc x=-2
d: =>2x+3=0
hay x=-3/2
1/phân tích thành phân tử
a. x^6 - 64
b. x^3+3x^2 + 3x+1- y^3
c. x^3 - 27+ x( x-3)
d, y^6 - 625
2/tìm x biết
a. 25x^2 -1=0
b. 4 (x-1)^2 -9 =0
c. 1/4 -9(x-1)^2 =0
d. 1/16 - ( 2x + 3/4) ^2 =0
1/4 nghĩa là 1 phần 4 á nhé, nhờ giúp đỡ
2/
a/ \(25x^2-1=0\)
<=> \(\left(5x\right)^2-1=0\)
<=> \(\left(5x-1\right)\left(5x+1\right)=0\)
<=> \(\orbr{\begin{cases}5x-1=0\\5x+1=0\end{cases}}\)<=> \(\orbr{\begin{cases}x=\frac{1}{5}\\x=-\frac{1}{5}\end{cases}}\)
b/ \(4\left(x-1\right)^2-9=0\)
<=> \(\left[2\left(x-1\right)\right]^2-3^2=0\)
<=> \(\left(2x-2\right)^2-3^2=0\)
<=> \(\left(2x-2-3\right)\left(2x-2+3\right)=0\)
<=> \(\left(2x-5\right)\left(2x+1\right)=0\)
<=> \(\orbr{\begin{cases}2x-5=0\\2x+1=0\end{cases}}\)<=> \(\orbr{\begin{cases}x=\frac{5}{2}\\x=-\frac{1}{2}\end{cases}}\)
c/ \(\frac{1}{4}-9\left(x+1\right)^2=0\)
<=> \(\left(\frac{1}{2}\right)^2-\left[3\left(x-1\right)\right]^2=0\)
<=> \(\left(\frac{1}{2}\right)^2-\left(3x-3\right)^2=0\)
<=> \(\left(\frac{1}{2}-3x+3\right)\left(\frac{1}{2}+3x-3\right)=0\)
<=> \(\left(\frac{7}{2}-3x\right)\left(-\frac{5}{2}+3x\right)=0\)
<=> \(\orbr{\begin{cases}\frac{7}{2}-3x=0\\-\frac{5}{2}+3x=0\end{cases}}\)<=> \(\orbr{\begin{cases}3x=\frac{7}{2}\\3x=\frac{5}{2}\end{cases}}\)
<=> \(\orbr{\begin{cases}x=\frac{7}{6}\\x=\frac{5}{6}\end{cases}}\)
d/ \(\frac{1}{16}-\left(2x+\frac{3}{4}\right)^2=0\)
<=> \(\left(\frac{1}{4}\right)^2-\left(2x+\frac{3}{4}\right)^2=0\)
<=> \(\left(\frac{1}{4}-2x-\frac{3}{4}\right)\left(\frac{1}{4}+2x+\frac{3}{4}\right)=0\)
<=> \(\left(-\frac{1}{2}-2x\right)\left(1+2x\right)=0\)
<=> \(2\left(-\frac{1}{4}-x\right)\left(1+2x\right)=0\)
<=> \(\orbr{\begin{cases}-\frac{1}{4}-x=0\\1+2x=0\end{cases}}\)<=> \(\orbr{\begin{cases}x=-\frac{1}{4}\\x=-\frac{1}{2}\end{cases}}\)
10 Phân tích các đa thức sau thành nhân tử:
a) 5xy(x-y)-2x+2y ; b) 6x-2y-x(y-3x)
c) x^2+4x-xy-4y ; d) 3xy+2z-6y-xz
11 Tìm x, biết: a) 4-9x^2=0 ; b) x^2+x+1/4=0 ; c) 2x(x-3)+(x-3)=0
d) 3x(x-4)-x+4=0 ; e) x^3-1/9x=0 ; f) (3x-y)^2-(x-y)^2=0
a) 5xy ( x - y ) - 2x + 2y
= 5xy ( x - y ) - 2 ( x - y )
= ( x - y ) ( 5xy - 2 )
b) 6x-2y-x(y-3x)
= 2 ( y - 3x ) - x ( y - 3x )
= ( y - 3x ( ( 2 - x )
c) x2 + 4x - xy-4y
= x ( x + 4 ) - y ( x + 4 )
( x + 4 ) ( x - y )
d) 3xy + 2z - 6y - xz
= ( 3xy - 6y ) + ( 2z - xz )
= 3y ( x - 2 ) + z ( x - 2 )
= ( x - 2 ) ( 3y + z )
a,5xy(x-y)-2x+2y=5xy(x-y)-2(x-y)=(x-y)(5xy-2)
b,6x-2y-x(y-3x)=-2(y-3x)-x(y-3x)=(y-3x)(-2-x)
c,x^2+4x-xy-4y=x(x+4)-y(x+4)=(x+4)(x-y)
d,3xy+2z-6y-xz=(3xy-6y)+(2z-xz)=3y(x-2)+z(2-x)=3y(x-2)-z(x-2)=(x-2)(3y-z)
11)
a,4-9x^2=0
(2-3x)(2+3x)=0
2-3x=0=>x=2/3 hoặc 2+3x=0=>x=-2/3
b,x^2 +x+1/4=0
(x+1/2)^2 =0
x+1/2=0
x=-1/2
c,2x(x-3)+(x-3)=0
(x-3)(2x+1)=0
x-3=0=>x=3 hoặc 2x+1=0=>x=-1/2
d,3x(x-4)-x+4=0
3x(x-4)-(x-4)=0
(x-4)(3x-1)=0
x-4=0=>x=4 hoặc 3x-1=0=>x=1/3
e,x^3-1/9x=0
x(x^2-1/9)=0
x(x+1/3)(x-1/3)=0
x=0 hoặc x+1/3=0=>x=-1/3 hoặc x-1/3=0=>x=1/3
f,(3x-y)^2-(x-y)^2 =0
(3x-y-x+y)(3x-y+x-y)=0
2x(4x-2y)=0
4x(2x-y)=0
x=0hoặc 2x-y=0=>x=y/2
Phân tích đa thức thành nhân tử
x^8+x^6+x^4+x^2+1
Cho a^2+b^2=c^2+d^2=2016 và a×d = b×c=0
Tính(a×b)+(c×d)
bài 1: Tìm x
a)5(x-1)=x-1
b)x(x-2)+(x-2)=0
c)5x(x-3)-x+3=0
d)x(2x-7)-4x+17=0
bai2:phân tích thành nhân tử
a)2x^2+2y-x^2z+z-y^2z-2
a) 5(x-1)=x-1
5x-5=x-1
5x-x=5-1
4x=4=>x=1
b)x(x-2)+(x-2)=0
(x-2)(x+1)=0
=>x=2 hay x=-1
c)5x(x-3)-x+3=0
5x(x-3)-(x-3)=0
(5x-1)(x-3)=0
=>x=\(\frac{1}{5}\)hay x=3
d)x(2x-7)-4x+17=0
x(2x-7-4)+17=0
x(2x-11)+17=0
=> đa thức này không có nghiệm
1) phân tích thành phân tử:
a) x^3y^3 + 1/125
b) (x+5)^3-(x-5)^3
c) (6-x)^3+(6+x)^3
d) 27x^3 -135x^2+225x-125
2) tìm x:
a)4x^2-25x^4=0
b) x^2-8x+16=0
c)x^3-3x^2+3x-1=0
1.
a) = (xy + \(\frac{1}{5}\)) (x2y2 - \(\frac{xy}{5}\)+ \(\frac{1}{25}\))
b) = (x + 5 - x + 5) [(x+5)2 + (x+5)(x-5) + (x-5)2] = 10 (x2 + 10x + 25 + x2 - 25 + x2 - 10x + 25) = 10 (3x2 +25)
c) = (6 - x + 6 + x) [(6-x)2 - (6-x)(6+x) + (6+x)2] = 12 (36 - 12x + x2 - 26 + x2 + 36 + 12x + x2) = 12 (3x2 + 36) = 12. 3(x2 + 12) = 36(x2 +12)
d) = (3x - 5)3
2.
a) => (2x - 5x2)(2x + 5x2) = 0 ............. giải ra
b) => (x-4)2 = 0 => x - 4 = 0 => x= 4
c) => (x - 1)3 = 0 => x - 1 = 0 => x = 1
1.Phân tích đa thức thành nhân tử
a, x^3z+x^2yz-x^2z^2-xyz^2
b, x^3+x^2y-x^2z-xyz
c, a^2x+a^2y+ax+ay+x+y
d, xa+xb+ya+yb-za-zb
2.Phân tích đa thức thành nhân tử
a, a^2+2ab+b^2-c^2+2cd-d^2
b, x^2-4xy+4y^2-x+2y
c,2^2-(x-1)^2+2(x-1)-1
d, xz-yz-x^2+2xy-y^2
3.Tìm x biết
a, x(2x-7)-4x+14 = 0
b, x(x-1)+2x-2 = 0
c, x+x^2-x^2-x^4 = 6
d, 2x^3+3x^2+2x+3 =0
Các bạn giúp mình đi mà. Hu hu![]()
Bạn phải bấm rõ mình mới giúp dc, nhìn vào ko hỉu lắm
Đây bạn nhé, bạn dùng phương pháp nhóm hạng tử rồi phân tích đa thức thành nhân tử thôi mà bạn. Tớ chỉ gợi ý một số câu, những câu còn lại bạn tự rèn luyện nhé. Mình gửi bạn nhé. ![]() . Bạn cũng kiểm tra lại xem mình có sai xót chỗ nào không nhé
. Bạn cũng kiểm tra lại xem mình có sai xót chỗ nào không nhé

 câu 1a) KQ= (x+y)(x-z)xz
câu 1a) KQ= (x+y)(x-z)xz
1b)=x(x+y)(x-z)
2d)=(x-y)(z-x+y)
3b)x1=1; x2= - 2
3c)x1=0; x2= - 1 ( trường hợp x2 +1=0 loại vì vô lý )
3d) x = - 3/2 ( trường hợp x2 +1=0 loại vì vô lý )
Phân tích thành nhân tử
a. x2 - 7
b.4x2 - 5
c.3x2 - 1
d. x - 1 với x>= 0
e. x-4 với x>=0
f. 9x-4 với x>=0
Bài làm:
a) \(x^2-7=\left(x-\sqrt{7}\right)\left(x+\sqrt{7}\right)\)
b) \(4x^2-5=\left(2x-\sqrt{5}\right)\left(2x+\sqrt{5}\right)\)
c) \(3x^2-1=\left(x\sqrt{3}-1\right)\left(x\sqrt{3}+1\right)\)
d) \(x-1=\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\)
e) \(x-4=\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\)
f) \(9x-4=\left(3\sqrt{x}-2\right)\left(3\sqrt{x}+2\right)\)
. Bài 1: Phân tích đa thức thành nhân tử
a; A = x^3-2x^2-5x+6
b; B = x^4+5x^2+6
c; C = x^4-2x^3+2x-1
d; D = x^3+4x^2+5x+2
. Bài 2: Tìm x
a; x^3-9x^2+14x=0
b; x^3-5x^2+8x-4=0
c; x^4-2x^3+x^2=0
d; 2x^3+x^2-4x-2=0
1. Phân tích đa thức thành nhân tử: a) (x+4)^2+8x(x+4)^3+15x^2
2. Tìm x: a) 3x(x-2020)-x+2020=0
b)(2x-3).(3x+2)-6x^2=1
c)(3x-1)^2-(x+5)^2=0
d)4x^2-4x-35=0