Tìm tất cả các giá trị thực của tham số m để hàm số y = 2017 2018 e 3 x - ( m - 1 ) e x + 1 đồng biến trên khoảng (1;2)?
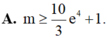
![]()
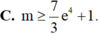
![]()
1. Tìm tất cả các giá trị thực của tham số m để hàm số y= mx - sin3x đồng biến trên khoảng ( trừ vô cùng ; cộng vô cùng) 2. Tìm tất cả các giá trị thực của tham số m để hàm số y = x + mcosx đồng biến trên khoảng( trừ vô cùng ; cộng vô cùng)
1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Tìm tất cả các giá trị của tham số m để hàm số y = 1 3 x 3 - m x 2 + m + 6 + x + 2017 * có 5 điểm cực trị.
A. m < - 2 ∪ m > 5
B. m > -6
C.m > 0
D.m > 3
Tìm tất cả các giá trị thực của tham số m để đường thẳng y = 2 m x − 2 m − 2028 cắt đồ thị hàm số y = x 3 − 3 x 2 − 9 x − 2017 tại 3 điểm phân biệt A,B,C sao cho AB=BC
A. − 6 < m < 1
B. m<-6 hoặc m>1
C. m ≥ 1
D. m > − 6
Đáp án D
Xét phương trình hoành độ giao điểm
x 3 − 3 x 2 − 9 x − 2017 = 2 m x − 2 m − 2028
⇔ x 3 − 3 x 2 − 9 + 2 m x + 2 m + 11 = 0
⇔ x − 1 x 2 − 2 x − 2 m − 11 = 0 ⇔ x = 1 x 2 − 2 x − 2 m − 11 = 0 2
2 đồ thị hàm số cắt nhau tại 3 điểm nếu (2) có 2 nghiệm phân biệt
⇔ = 1 + 2 m + 11 > 0 ⇔ m > − 6
Khi đó 2 nghiệm của phương trình là x 1 ; x 2 thỏa mãn x 1 + x 2 = 2 nên chắc chắn 3 điểm cắt nhau sẽ thỏa mãn A B = B C (B là trung điểm của ).
Tìm tất cả các giá trị thực của tham số m để hàm số y = x e x 2 + m x - 2 có cực trị
A. m ∈ ℝ
B. m > 2 2
C. m ≠ 0
D. m > 2 2
Chọn D.
Phương pháp: Tính đạo hàm và tìm điều kiện để hàm số có cực trị.
Cách giải: Ta có:
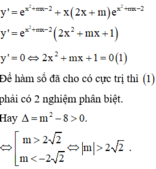
Tìm tất cả các giá trị thực của tham số m để hàm số y = x e x 2 + m x - 2 có cự trị
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y = m - 1 x 4 + 2 m 2 + 1 có một cực trị
A. m ≤ 0 v à m ≥ 1
B. m < 0 v à m > 1
C. 0 ≤ m < 1
D. m ≤ 0 v à m > 1
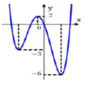
Cho hàm số y = f (x) có đồ thị như hình bên. Gọi S là tập tất cả các giá trị nguyên dương của tham số m để hàm số y = f x - 2018 + m có 5 điểm cực trị. Tổng tất cả các giá trị của tập S bằng
A. 9
B. 7
C. 12
D. 18
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) + m - 2018 = 0 có duy nhất một nghiệm.
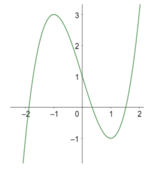
A. m ≤ 2015, m ≥ 2019.
B. 2015 < m < 2019.
C. m = 2015, m = 2019.
D. m < 2015, m > 2019.
Chọn D
Phương pháp:
Biến đổi phương trình về f(x) = 2018 - m và sử dụng tương giao đồ thị: Phương trình có duy nhất một nghiệm khi và chỉ khi đường thẳng y = 2018 - m cắt đồ thị hàm số y = f(x) tại duy nhất một điểm.
Cách giải:
Phương trình f(x) + m - 2018 = 0 ![]()
Đây là phương trình hoành độ giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = 2018 - m (có phương song song hoặc trùng với trục hoành).
Dựa vào đồ thị, ta có ycbt 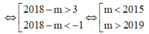
Cho hàm số y=f(x) xác định trên R và có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x)+m-2018=0 có duy nhất một nghiệm.
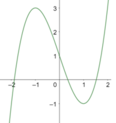
A. m ≤ 2015 , m ≥ 2019 .
B.2015<m<2019
C.m=2015,m=2019
D.m<2015,m>2019