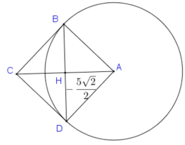
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF:
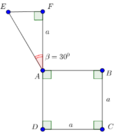
A. 10 π 7 a 3
B. π 3 a 3
C. 5 π 2 a 3
D. 10 π 9 a 3
Những câu hỏi liên quan
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF. A.
10
πa
3
9
B.
10
πa
3
7
C.
5
πa
3
2
D.
πa...
Đọc tiếp
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF.
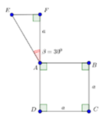
A. 10 πa 3 9
B. 10 πa 3 7
C. 5 πa 3 2
D. πa 3 3
Chọn A.
Phương pháp: Ta thấy vật thể tròn xoay gồm 2 phần nón và trụ.
Cách giải:
Đúng 0
Bình luận (0)
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF
Đọc tiếp
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF : A.
10
π
7
a
3
.
B.
π
3
a
3
.
C.
5
π...
Đọc tiếp
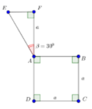
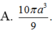
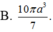
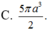
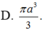
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF :
A. 10 π 7 a 3 .
B. π 3 a 3 .
C. 5 π 2 a 3 .
D. 10 π 9 a 3 .
Đáp án là D
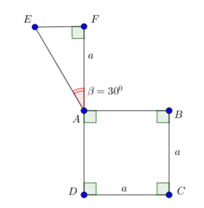
Quay hình vuông ABCD quanh trục DF ta được một hình trụ có bán kính bằng đường cao bằng a có thể tích V 1 = π a 3 .
Trong tam giác vuông AEF có EF =AF . tan 30 ° = a 3 .
Quay tam giác AEF quanh trục AEF ta được một hình nón có bán kính đáy
EF = a 3 và đường cao AF = a có thể tích V 2 = 1 3 π a 2 3 a = π a 3 9 .
Vậy thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh
trục DF là: V 1 + V 2 = π a 3 + π a 3 9 = 10 π a 3 9
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết
A
B
4
,
A
D
7
. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN. A.
104
3
π
B.
116
3
π
C.
44
3
π
D....
Đọc tiếp
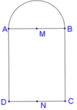
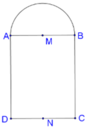
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết A B = 4 , A D = 7 . Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
A. 104 3 π
B. 116 3 π
C. 44 3 π
D. 1000 3 π
Đáp án D
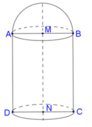
Khi quay mô hình đã cho quanh trục MN ta được một khối tròn xoay gồm:
- hình trụ có chiều cao là AD, đáy là hình tròn , có thể tích V 1 ;
- nửa hình cầu tâm M bán kính MA, có thể tích V 2
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M,N lần lượt là trung điểm của AB,CD. Biết
AB
4
,
AD
7
. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN. A.
44
3
π
B.
24
3
π
C.
100
3
π
D. ...
Đọc tiếp
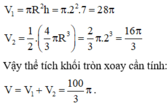
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M,N lần lượt là trung điểm của AB,CD. Biết AB = 4 , AD = 7 . Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
A. 44 3 π
B. 24 3 π
C. 100 3 π
D. 116 3 π
Đáp án C
Khi quay mô hình đã cho quanh trục MN ta được một khối tròn xoay gồm:
- hình trụ có chiều cao là AD, đáy là hình tròn (M,MA), có thể tích V 1 ;
- nửa hình cầu tâm M bán kính MA, có thể tích V 2 .
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết AB 4,AD 7. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
Đọc tiếp
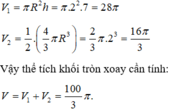
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết AB = 4,AD = 7. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
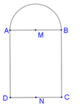
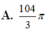
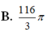
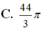
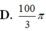
Chọn D
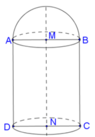
Khi quay mô hình đã cho quanh trục MN ta được một khối tròn xoay gồm:
- hình trụ có chiều cao là AD, đáy là hình tròn(M,MA), có thể tích V 1 ;
- nửa hình cầu tâm M bán kính MA, có thể tích V 2
Đúng 0
Bình luận (0)
Cho hai hình vuông có cùng cạnh bằng 5 được xếp chồng lên nhau sao cho đỉnh X của một hình vuông là tâm của hình vuông còn lại (như hình vẽ). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên xung quanh trục XY.
Đọc tiếp
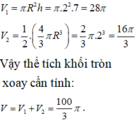
Cho hai hình vuông có cùng cạnh bằng 5 được xếp chồng lên nhau sao cho đỉnh X của một hình vuông là tâm của hình vuông còn lại (như hình vẽ).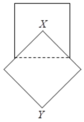 
Tính thể tích V của vật thể tròn xoay khi quay mô hình trên xung quanh trục XY.
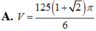
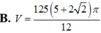
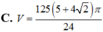
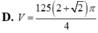
Tính thể tích của vật thể tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục Ox: y = 2x/ π ; y = sinx; x ∈ [0; π /2]
Trong mặt phẳng (P) cho hình vuông ABCD có cạnh bằng 5 và đường tròn (C) có tâm A, đường kính 10. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh trục là đường AC. A.
1000
π
+
375
π
2
6
B.
1000
π
+...
Đọc tiếp
Trong mặt phẳng (P) cho hình vuông ABCD có cạnh bằng 5 và đường tròn (C) có tâm A, đường kính 10. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh trục là đường AC.
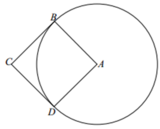
A. 1000 π + 375 π 2 6
B. 1000 π + 375 π 2 6
C. 500 π + 125 π 2 6
D. 500 π + 375 π 2 6
Đáp án B
Ta có thể tích vật thể tròn xoay được tạo ra S = S 1 + S 2 .
S 1 = π − 5 2 2 5 25 − x 2 2 d x = 500 π 3 .
S 2 = 1 3 π 5 2 2 3 = π .125.2 2 3.8 = 125 π 2 6
Vậy S = 1000 π + 125 π 2 6 .
Đúng 0
Bình luận (0)