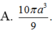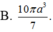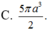Các câu hỏi tương tự
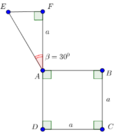
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF: A.
10
π
7
a
3
B.
π
3
a
3
C. ...
Đọc tiếp
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF:
A. 10 π 7 a 3
B. π 3 a 3
C. 5 π 2 a 3
D. 10 π 9 a 3
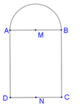
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết AB 4,AD 7. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
Đọc tiếp
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết AB = 4,AD = 7. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
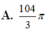
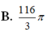
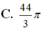
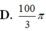
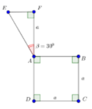
Cho hai hình vuông có cùng cạnh bằng 5 được xếp chồng lên nhau sao cho đỉnh X của một hình vuông là tâm của hình vuông còn lại (như hình vẽ). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên xung quanh trục XY.
Đọc tiếp
Cho hai hình vuông có cùng cạnh bằng 5 được xếp chồng lên nhau sao cho đỉnh X của một hình vuông là tâm của hình vuông còn lại (như hình vẽ). 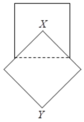
Tính thể tích V của vật thể tròn xoay khi quay mô hình trên xung quanh trục XY.
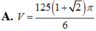
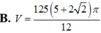
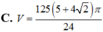
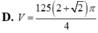
Cho tam giác vuông cân ABC có
A
B
A
C
a
2
và hình chữ nhật MNPQ với MQ2MN được xếp chồng lên nhau sao cho M, N lần lượt là trung điểm của AB, AC (như hình vẽ). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục AI, với I là trung điểm PQ.
Đọc tiếp
Cho tam giác vuông cân ABC có A B = A C = a 2 và hình chữ nhật MNPQ với MQ=2MN được xếp chồng lên nhau sao cho M, N lần lượt là trung điểm của AB, AC (như hình vẽ). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục AI, với I là trung điểm PQ.
![]()
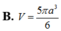
![]()
![]()
Trong mặt phẳng (P) cho hình vuông MNPQ có cạnh bằng 7 và hình tròn (C) có tâm M, đường kính bằng 14. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình trên quanh trục là đường thẳng PM.
Đọc tiếp
Trong mặt phẳng (P) cho hình vuông MNPQ có cạnh bằng 7 và hình tròn (C) có tâm M, đường kính bằng 14. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình trên quanh trục là đường thẳng PM.
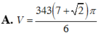
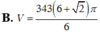
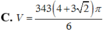
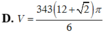
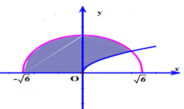
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số
y
x
, cung tròn có phương trình
y
6
-
x
2
(
-
6
≤
x
≤
6
)
và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng H quanh trục
Đọc tiếp
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x , cung tròn có phương trình y = 6 - x 2 ( - 6 ≤ x ≤ 6 ) và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng H quanh trục
![]()
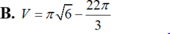
![]()
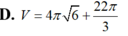
Cho tam giác đều và hình vuông cùng có cạnh bằng 4 được xếp chồng lên nhau sao cho một đỉnh của tam giác đều trùng với tâm của hình vuông, trục của tam giác đều trùng với trục của hình vuông (như hình vẽ). Thể tích của vật thể tròn xoay sinh bởi hình đã cho khi quay quanh trục AB là.
Đọc tiếp
Cho tam giác đều và hình vuông cùng có cạnh bằng 4 được xếp chồng lên nhau sao cho một đỉnh của tam giác đều trùng với tâm của hình vuông, trục của tam giác đều trùng với trục của hình vuông (như hình vẽ). Thể tích của vật thể tròn xoay sinh bởi hình đã cho khi quay quanh trục AB là.
![]()
![]()
![]()
![]()
Tính thể tích của vật thể tròn xoay sinh bởi hình phẳng trên quay quanh trục hoành.
Cho hình phẳng (H) giới hạn bởi các đường
y
x
+
2
,
y
x
+
2
,
x
1
. Tính thể tích V của vật thể tròn xoay khi quay hình (H) quanh trục hoành A.
V
27
π
2
B.
V
9
π
2...
Đọc tiếp
Cho hình phẳng (H) giới hạn bởi các đường y = x + 2 , y = x + 2 , x = 1 . Tính thể tích V của vật thể tròn xoay khi quay hình (H) quanh trục hoành
A. V = 27 π 2
B. V = 9 π 2
C. V = 9 π
D. V = 55 π 6