Cho hàm số y = f(x) xác định và có đạo hàm trên đoạn [0;2]. Biết rằng f(2) = -3 và ∫ 0 2 x f ' ( x ) d x = - 4  Tính tích phân I = ∫ 0 2 f ( x ) d x  

A. I = 2.

B. I = 0.

C. I = -7.

D. I = -2.

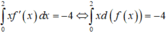
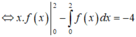
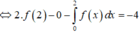
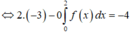
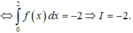
Cho hàm số y=f(x) là hàm lẻ, liên tục trên [-4;4], biết  ∫ - 2 0 f ( - x ) dx = 2 và  ∫ 1 2 f ( - 2 x ) dx = 4 . Tính I= 2 ∫ 0 4 f ( x ) dx

A. I = -10.

B. I = -6.

C. I = 6.

D. I = 10

Cho hàm số y = f(x) là hàm lẻ và liên tục trên [-4;4] biết ∫ - 2 0 f ( - x ) d x   =   2  và ∫ 1 2 f ( - 2 x ) d x   =   4 . Tính I   =   ∫ 0 4 f ( x ) d x .

A. I = 10

B. I = -6

C. I = 6

D. I = -10

Cho hàm số y = f(x) là hàm lẻ và liên tục trên [-4;4] biết ∫ - 2 0 f ( - x ) d x   =   2  và ∫ 1 2 f ( - 2 x ) d x   =   4  Tính  I   =   ∫ 0 4 f ( x ) d x

A. I = -10

B. I = -6

C. I = 6

D. I = 10

Cho hàm số f(x) là hàm số lẻ, liên tục trên [-4;4]. Biết rằng ∫ - 2 0 f ( - x ) d x = 2  và ∫ 1 2 f ( - 2 x ) d x = 4 . Tính tích phân I= ∫ 0 4 f ( x ) d x

Cho hàm số y = f ( x )  liên tục trên R. Biết f ( 2 ) = 4  và ∫ 0 2 f ( x ) d x = 5 . Tính  I = ∫ 0 2 x . f ' ( x ) d x

Biết  ∫ a b f ( x ) d x = 3 ,   ∫ b a g ( x ) d x = 5 . Tính  I = ∫ a b 3 f ( x ) + 2 g ( x ) d x

Tính các tích phân sau

1.I=\(\int\limits^{\frac{\Pi}{4}}_0\) (x+1)sin2xdx

2.I=\(\int\limits^2_1\frac{x^2+3x+1}{x^2+x}dx\)

3.I=\(\int\limits^2_1\frac{x^2-1}{x^2}lnxdx\)

4. I=\(\int\limits^1_0x\sqrt{2-x^2}dx\)

5.I=\(\int\limits^1_0\frac{\left(x+1\right)^2}{x^2+1}dx\)

6. I=\(\int\limits^5_1\frac{dx}{1+\sqrt{2x-1}}\)

7. I=\(\int\limits^3_1\frac{1+ln\left(x+1\right)}{x^2}dx\)

8.I=\(\int\limits^1_0\frac{x^3}{x^4+3x^2+2}dx\)

9. I=\(\int\limits^{\frac{\Pi}{4}}_0x\left(1+sin2x\right)dx\)

10. I=\(\int\limits^3_0\frac{x}{\sqrt{x+1}}dx\)

Biết  ∫ a b f ( x ) dx = 3 và ∫ b a g ( x ) dx = 5 . Tính I= ∫ a b [ 3 f ( x ) + 2 g ( x ) ] dx

A. I=19. 

B. I=-19.

C.  I=1.

D. I=-1