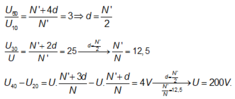Cho cấp số cộng u n biết u 5 = 18 v à 4 S n = S 2 n . Tìm số hạng đầu tiên u 1 và công sai d của cấp số cộng
A. u 1 = 2 ; d = 4
B. u 1 = 2 ; d = 3
C. u 1 = 2 ; d = 2
D. u 1 = 3 ; d = 2
Cho cấp số cộng (un) có u4=-12, u14=18. Tính tổng 16 số hạng đầu tiên cua cấp số cộng này
\(\left\{{}\begin{matrix}u_{14}=u_1+13d=18\\u_4=u_1+3d=-12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}d=3\\u_1=-21\end{matrix}\right.\)
Tổng 16 số hạng đầu tiên:
\(S_{16}=\frac{16\left(2u_1+15d\right)}{2}=24\)
Cho cấp số cộng (un) biết \(\left\{{}\begin{matrix}u_3=5\\S_8=48\end{matrix}\right.\) . Tìm số hạng đầu tiên và tổng 20 số hạng đầu của cấp số công đã cho.
cho (Un) là cấp số cộng U3 +U13=80 .tổng 15 số hạng đầu tiên của cấp số cộng đố bằng bao nhiêu
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
1. Cho 3 số lập thành cấp số cộng. Biết tổng 3 số bằng 6 và tổng bình phương 3 số bằng 30. Tìm các số.
2. Tìm m để phương trình sau có 4 nghiệm lập thành cấp số cộng:
\(x^4-10x^2+9m=0\)
3. Cho cấp số cộng giảm thỏa mãn:
\(\left\{{}\begin{matrix}u_1+u_2+u_3=3\\u_3^2-u_2^2=3\end{matrix}\right.\)
Tính: \(S=\dfrac{1}{u_1u_2}+\dfrac{1}{u_2u_3}+...+\dfrac{1}{u_{19}u_{20}}\)
4. Cho cấp số cộng tăng:
\(\left\{{}\begin{matrix}u_1+u_3+u_5=-3\\u_2+u_4+u_6=3\end{matrix}\right.\)
Tính: \(S=u_1+u_4+u_7+...+u_{88}\)
Mọi người giúp mình với ạ!!! Mình cảm ơn mọi người nhiều!!!
Câu 1: Gọi 3 số là a;b;c
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=6\\2b=a+c\\a^2+b^2+c^2=30\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\a+c=4\\a^2+c^2=26\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}b=2\\c=4-a\\a^2+\left(4-a\right)^2=26\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\c=5\\a=-1\end{matrix}\right.\left(\text{V\text{ì} }a< c\right)\)
Câu 2: Đặt \(t=x^2\left(t\ge0\right)\)
\(pt:x^4-10\text{x}^2+9m=0\left(1\right)\\ \Leftrightarrow t^2-10t^2+9m=0\left(2\right)\)
Để pt(1) có 4 nghiệm lập thành cấp số cộng thì (2) phải có 2 nghiệm dương phân biệt
\(\)\(\Rightarrow\left\{{}\begin{matrix}\Delta'=\left(-5\right)^2-9m>0\\S=10>0\left(T/m\right)\\P=9m>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m< \dfrac{25}{9}\\\\m>0\end{matrix}\right.\\ \Rightarrow0< m< \dfrac{25}{9}\)
(2) có 2 nghiệm \(t_1< t_2\)
=> (1) có 4 nghiệm \(-\sqrt{t_2}< -\sqrt{t_1}< \sqrt{t_1}< \sqrt{t_2}\)
\(\Rightarrow\sqrt{t_1}=\sqrt{t_2}-\sqrt{t_1}\\ \Rightarrow4t_1=t_2\\ \Rightarrow\left\{{}\begin{matrix}t_1+t_2=10\\4t_1=t_2\\t_1t_2=9m\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}t_1=2\\t_2=8\\m=\dfrac{16}{9}\left(t/m\right)\end{matrix}\right.\)
Câu 2: Đặt \(t=x^2\left(t\ge0\right)\)
\(pt:x^4-10\text{x}^2+9m=0\left(1\right)\\ \Leftrightarrow t^2-10t^2+9m=0\left(2\right)\)
Để pt(1) có 4 nghiệm lập thành cấp số cộng thì (2) phải có 2 nghiệm dương phân biệt
\(\)\(\Rightarrow\left\{{}\begin{matrix}\Delta'=\left(-5\right)^2-9m>0\\S=10>0\left(T/m\right)\\P=9m>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m< \dfrac{25}{9}\\\\m>0\end{matrix}\right.\\ \Rightarrow0< m< \dfrac{25}{9}\)
(2) có 2 nghiệm \(t_1< t_2\)
=> (1) có 4 nghiệm \(-\sqrt{t_2}< -\sqrt{t_1}< \sqrt{t_1}< \sqrt{t_2}\)
\(\Rightarrow\sqrt{t_1}=\sqrt{t_2}-\sqrt{t_1}\\ \Rightarrow4t_1=t_2\\ \Rightarrow\left\{{}\begin{matrix}t_1+t_2=10\\4t_1=t_2\\t_1t_2=9m\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}t_1=2\\t_2=8\\m=\dfrac{16}{9}\left(t/m\right)\end{matrix}\right.\)
a) Xác địch x,y trong cấp số cộng sau: x ; 4 ; y ; 4x ; 10 ; 2y ; 14 ; ...
b) Từ cấp số cộng trên tìm số hạng Un để Sn = 420.
Lời giải:
a) Theo tính chất về cấp số cộng là \(u_k=\frac{u_{k-1}+u_{k+1}}{2}\) thì có:
\(\left\{\begin{matrix} y=\frac{4+4x}{2}=2x+2\\ 2y=\frac{10+14}{2}=12\end{matrix}\right.\Rightarrow \left\{\begin{matrix} y=6\\ x=2\end{matrix}\right.\)
Vậy ta thu được dãy $(u_n)$: \(2,4,6,8,10,12,14,.....\) với \(u_n=2n\)
\(S_n=u_1+u_2+...+u_n=2.1+2.2+2.3+...+2n\)
\(=2(1+2+3+...+n)=2.\frac{n(n+1)}{2}=n(n+1)\)
Để \(S_n=420\Rightarrow n(n+1)=420\)
\(\Rightarrow n=20\)
Do đó \(U_n=U_{20}=2.20=40\)
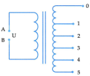
Đặt vào hai đầu A, B một máy biến áp lí tưởng của một điện áp xoay chiều có giá trị hiệu dụng U không đổi. Biết các cuộn dây vòng thứ cấp tăng từ mức 1 đến mức 5 theo cấp số cộng. Dùng vôn kế xoay chiều lý tưởng đo điện áp hiệu dụng ở đầu ra của cuộn thứ cấp thì thu được kết quả sau: U 50 = 3 U 10 , U 40 - U 20 = 4 V , 25 U 30 = U . Giá trị của U là
A. 200V
B. 240V
C. 220V
D. 183V
Đáp án A
Giả sử số vòng dây của cuộn sơ cấp là N, số vòng dây nhỏ nhất của cuộn thứ cấp ứng với mức 01 là N’ và công sai của cấp số cộng là D.
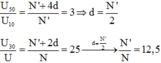
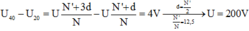
Đặt vào hai đầu A, B một máy biến áp lí tưởng của một điện áp xoay chiều có giá trị hiệu dụng U không đổi. Biết các cuộn dây vòng thứ cấp tăng từ mức 1 đến mức 5 theo cấp số cộng. Dùng vôn kế xoay chiều lý tưởng đo điện áp hiệu dụng ở đầu ra của cuộn thứ cấp thì thu được kết quả sau: U 50 = 3 U 10 , U 40 − U 20 = 4 V , 25 U 30 = U . Giá trị của U là:
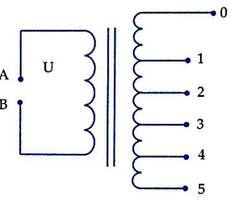
A. 200 V
B. 240 V
C. 220 V
D. 183 V
Đáp án A
Giả sử số vòng dây của cuộn sơ cấp là N, số vòng dây nhỏ nhất của cuộn thứ cấp ứng với mức 01 là N' và công sai của cấp số cộng là d
U 50 U 10 = N ' + 4 d N ' = 3 ⇒ d = N ' 2 U 30 U = N ' + 2 d N ' = 25 → d = N ' 2 N ' N = 12 , 5 U 40 − U 20 = U . N ' + 3 d N − U . N ' + d N = 4 V → N ' N = 12 , 5 d = N ' 2 U = 200 V
Đặt vào hai đầu A, B một máy biến áp lí tưởng của một điện áp xoay chiều có giá trị hiệu dụng U không đổi. Biết các cuộn dây vòng thứ cấp tăng từ mức 1 đến mức 5 theo cấp số cộng. Dùng vôn kế xoay chiều lý tưởng đo điện áp hiệu dụng ở đầu ra của cuộn thứ cấp thì thu được kết quả sau: U 50 = 3 U 10 , U 40 - U 2 0 = 4 V , 25 U 30 = U . Giá trị của U là
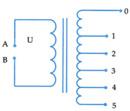
A. 200V
B. 240V
C. 220V
D. 183V
Đặt vào hai đầu A, B một máy biến áp lí tưởng của một điện áp xoay chiều có giá trị hiệu dụng U không đổi. Biết các cuộn dây vòng thứ cấp tăng từ mức 1 đến mức 5 theo cấp số cộng. Dùng vôn kế xoay chiều lý tưởng đo điện áp hiệu dụng ở đầu ra của cuộn thứ cấp thì thu được kết quả sau:
U 50 = 3 U 10 , U 40 - U 20 = 4 V , 25 U 30 = U
Giá trị của U là:
A. 200 V.
B. 240 V.
C. 220 V.
D. 183 V.
Đáp án A.
Lời giải chi tiết:
Giả sử số vòng dây của cuộn sơ cấp là N, số vòng dây nhỏ nhất của cuộn thứ cấp ứng với mức 01 là N’ và công sai của cấp số cộng là d.