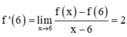Cho hàm số y = f ( x ) thỏa mãn: f ( 2 x - 1 x + 2 ) = 3 x + 5 2 x - 1 ( x ≠ 2 ; 1 2 ) . Tìm lim x → + ∞ f ( x )
A. 4 3
B. 1 5
C. 3 2
D. 2 3
Cho hàm số y=f(x) thỏa mãn f(x)+3f(1/x)=x^2. Tính f(2)
Cho hàm số y = f ( x ) thỏa mãn f ( 2 ) = 1 4 và f ' ( x ) = 2 x . [ f ( x ) ] 2 với ∀ x ∈ R tính f ( 1 )
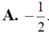
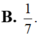
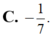
![]()
Xét các khẳng định sau
i) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại α ∈ - 1 ; 1 thỏa mãn f ( x ) ≥ f ( α ) ∀ x ∈ - 1 ; 1 .
ii) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại β ∈ - 1 ; 1 thỏa mãn f ( x ) ≤ f ( β ) ∀ x ∈ - 1 ; 1 .
iii) Nếu hàm số y = f(x) xác định trên [-1;1] thỏa mãn f(-1).f(1)<0 thì tồn tại γ ∈ - 1 ; 1 thỏa mãn f ( γ ) = 0
Số khẳng định đúng là
A. 3.
B. 2.
C. 1.
D. 0.
Cho đồ thị hàm số y = f(x) có đạo hàm trên R thỏa mãn f(2) = f(-2) = 0 và đồ thị hàm số y = f'(x) có dạng như hình vẽ. Hàm số y = f ( x ) 2 nghịch biến trên khoảng nào trong các khoảng sau?
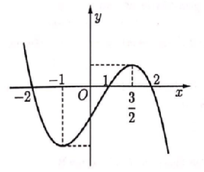
A. - 1 ; 3 2
B. (-2;-1)
C. (-1;1)
D. (1;2)
Cho hàm số y = f(x) thỏa mãn f(2) = 1 4 và f ' ( x ) = 2 x f ( x ) 2 với ∀ x ∈ R , tính f(1)
A. - 1 2
B. 1 7
C. - 1 7
D. 7
Cho hàm số y=f(x) có đạo hàm dương trên [1;2] thỏa mãn f ( 1 ) = 1 e và x f ' ( x ) + ( x + 1 ) f ( x ) = 3 x 2 e - x . Tính f(2)
A. f ( 2 ) = 1 e 2
B. f ( 2 ) = 2 e 2
C. f ( 2 ) = 4 e 2
D. f ( 2 ) = 8 e 2
Cho hàm số y=f(x) có đạo hàm liên tục trên ( 0 ; + ∞ ) thỏa mãn f ' ( x ) + f ( x ) x = 4 x 2 + 3 x và f(1)=2. Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x = 2 là x
A. y = 16x+20.
B. y = -16x+20
C. y = -16x-20
D. y = 16x-20.
Cho hàm số y = f(x) có đạo hàm trên ℝ , thỏa mãn f(2) = f(-2) =2019. Hàm số y = f'(x) có đồ thị hàm số như hình vẽ. Hỏi hàm số g(x)= f x - 2019 2 (1;2). Ngịch biến trên khoảng nào dưới đây
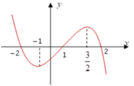
A . 1 ; 2
B . - 2 ; 2
C . 2 ; + ∞
D . - 2 ; - 1
Cho hàm số y=f(x) có đạo hàm trên R thỏa mãn f(-1)= f(3)= 0 và đồ thị hàm số y=f' (x) có dạng như hình vẽ. Hàm số y= [ f ( x ) ] 2 nghịch biến trên khoảng nào trong các khoảng sau?
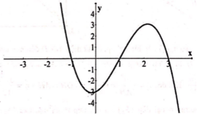
A. (-2;1).
B. (1;2).
C. (0;4).
D. (-2;2).
Cho hàm số y = f(x) có đạo hàm thỏa mãn f’(6) = 2. Giá trị biểu thức lim x → 6 f ( x ) - f ( 6 ) x - 6 bằng:
A. 2
B. 1/3
C. 1/2
D. 12
Đáp án A
Phương pháp:
Sử dụng công thức tính đạo hàm bằng định nghĩa: 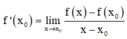 (nếu tồn tại giới hạn).
(nếu tồn tại giới hạn).
Cách giải: Ta có: