Đáp án A
Phương pháp:
Sử dụng công thức tính đạo hàm bằng định nghĩa: 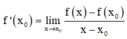 (nếu tồn tại giới hạn).
(nếu tồn tại giới hạn).
Cách giải: Ta có: 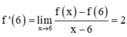
Đáp án A
Phương pháp:
Sử dụng công thức tính đạo hàm bằng định nghĩa: 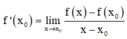 (nếu tồn tại giới hạn).
(nếu tồn tại giới hạn).
Cách giải: Ta có: 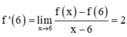
Cho hàm số f (x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;2] thoả mãn f(0)=3,f(2)=12 và ∫ 0 2 ( f ' ( x ) ) 2 f ( x ) d x = 6 . Tính f(1).
A. 27 4
B. 25 4
C. 9 2
D. 15 4
Cho hàm số f(x) xác định trên R \ { - 1 ; 1 } thỏa mãn f ' ( x ) = 2 x x 2 - 1 và f ( - 2 ) = 3 , f ( - 1 2 ) = 2 . Giá trị của biểu thức f ( - 2 ) + f ( 1 2 ) bằng
A. 15 + ln 9 2
B. ln 9 2
C. 5 + ln 9 2
D. 2 + ln 9 2
Cho hàm số y=f(x) có đạo hàm y ' = x 2 - 12 x + 1 4 ( b + 3 a ) ∀ x ∈ R , biết hàm số luôn có hai cực với a, b là các số thực không âm thỏa mãn 3 b - a ≤ 6 . Tìm giá trị lớn nhất của biểu thức P = 2a+b
A. 1
B. 9
C. 8
D. 6
Cho hàm số f(x) xác định trên R\{-1;2} thỏa mãn f ' ( x ) = 3 x 2 - x - 2 , f(-2)=2 ln2+2 và f(0)=ln2-1. Giá trị của biểu thức f(-3)+f( 1 2 ) bằng
A. 2+ln5.
B. 2+ln 5 2 .
C. 2-ln2.
D. 1+ln 5 2 .
Cho hàm số y=f(x) xác định trên R \ 1 2 thỏa mãn f ' ( x ) = 2 2 x - 1 , f ( 0 ) = 1 . Giá trị của biểu thức f ( - 1 ) + f ( 3 ) bằng:
A. 4+ln15
B. 2+ln15
C. 3+ln15
D. ln15
Cho hàm số y = f(x) liên tục trên khoảng - ∞ ; + ∞ , thỏa mãn các điều kiện l i m x → 0 f x x = 2 và hàm số y = f 2 x sin 2 x k h i x > 0 a x + b k h i x ≤ 0 có đạo hàm tại điểm x = 0 Giá trị của biểu thức a + b bằng
A. 2
B. 3
C. 0
D. 1
Cho hàm số y = f(x) đạo hàm f’(x) = –x2 – 1. Với các số thực dương a, b thỏa mãn a<b. Giá trị nhỏ nhất của hàm số f(x) trên đoạn [a;b] bằng
A. f(b)
B. f( a b )
C. f(a)
D. f( a + b 2 )
Cho hàm số f (x) nhận giá trị dương, có đạo hàm liên tục trên khoảng ( 0 ; + ∞ ) thỏa mãn 2 f ' ( x ) ( f ( x ) ) 2 = f ( x ) ( x + 2 ) x 3 , ∀ x > 0 và f ( 1 ) = 1 3 . Tích phân ∫ 1 2 1 ( f ( x ) ) 2 d x bằng
A. 11 2 +ln2
B. - 1 2 +ln2
C. 3 2 +ln2
D. 7 2 +ln2
Cho hàm số f(x) có đạo hàm trên R\{0} thỏa mãn f ' ( x ) + f ( x ) x = x 2 và f(1)=1 Giá trị của f ( 3 2 ) bằng
A. 1 96
B. 1 64
C. 1 48
D. 1 24