Cho hàm số y = f ( x ) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f sin x = m có nghiệm thuộc khoảng là
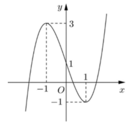
A. (-1;3)
B. (-1;1)
C. (-1;3)
D. (-1;1)
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sinx)=m có nghiệm thuộc khoảng 0 ; π là
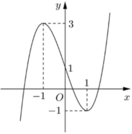
A. (-1;3)
B. (-1;1)
C. (-1;3)
D. (-1;1)
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(f(sinx))=m có nghiệm thuộc khoảng 0 ; π là
A. [-1;3)
B. (-1;1)
C. (-1;3]
D. [-1;1)
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(2sinx+1)=m có nghiệm thuộc nửa khoảng [ 0 ; π 6 ) là

A. (-2;0]
B. (0;2]
C. [-2;2]
D. (-2;0)
Đặt t=2sinx+1 với
![]()
![]()
![]()
Phương trình trở thành: f(t)=m có nghiệm ![]()
Chọn đáp án A.
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f ( e x ) = m có nghiệm thuộc khoảng (0;ln3):
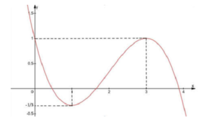
A. (1;3)
B. - 1 3 ; 0
C. - 1 3 ; 1
D. - 1 3 ; 1
Cho hàm số y = f (x) liên tục trên ℝ và có đồ thị như hình vẽ bên.
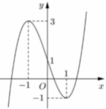
Tập hợp tất cả các giá trị thực của tham số m để phương trình f (sinx) = m có nghiệm thuộc khoảng (0; π ) là
A. [-1;3)
B. (-1;1)
C. (-1;3)
D. [-1;1 )
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sin x) = m có nghiệm thuộc khoảng 0 ; π là

![]()
![]()
![]()
![]()
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ
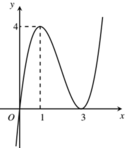
Tập hợp tất cả các giá trị thực của m để phương trình f e x 2 = m có đúng hai nghiệm thực là
A. 0 ∪ 4 ; + ∞
B. [0;4]
C. [4;+∞)
D. {0;4}
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(cosx)=10 có 2 nghiệm phân biệt thuộc ( 0 ; 3 π 2 ] là
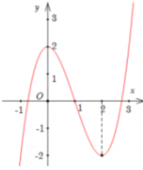
A. [-2;2]
B. (0;2)
C. (-2;2)
D. [0;2)
Chọn đáp án B
Phương pháp
+) Đặt t=cosx, xác định khoảng giá trị của t, khi đó phương trình trở thành f(t)=m.
+) Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(t) và y=m song song với trục hoành.
Cách giải
Đặt t=cosx ta có
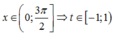
Khi đó phương trình trở thành f(t)=m.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(t) và y=m song song với trục hoành.
Dựa vào đồ thị hàm số y=f(x) ta thấy phương trình f(t)=m có 2 nghiệm phân biệt thuộc [-1;1) khi và chỉ khi mÎ(0;2).
Cho hàm số f(x) liên tục trên và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình có nghiệm thuộc khoảng ( 0 ; π ) là

A. [-4;-2]
B. [-4;0]\{2}
C. [-4;-2)
D. (-4;-2]
Đặt t = sin x ∈ ( 0 ; 1 ] , ∀ x ∈ ( 0 ; π ) Phương trình trở thành: f(t)=m(1)
Ta cần tìm m để (1) có nghiệm thuộc khoảng ( 0 ; 1 ] ⇔ - 4 ≤ m < - 2
Chọn đáp án C.