*) x² - 6 = x (1)

\(\Leftrightarrow\) x² - x - 6 = 0

\(\Leftrightarrow\) x² - 3x + 2x - 6 = 0

\(\Leftrightarrow\) x(x - 3) + 2(x - 3) = 0

\(\Leftrightarrow\) (x - 3)(x + 2) = 0

\(\Leftrightarrow\) x - 3 = 0 hoặc x + 2 = 0

\(\Leftrightarrow\) x = 3 và x = -2

Vậy S = {3; -2}

*) x² - 3x - 10 = 0 (2)

\(\Leftrightarrow\) x² - 5x + 2x - 10 = 0

\(\Leftrightarrow\) x(x + 2) - 5(x + 2) = 0

\(\Leftrightarrow\) (x + 2)(x - 5) = 0

\(\Leftrightarrow\) x + 2 = 0 hoặc x - 5 = 0

\(\Leftrightarrow\) x = -2 và x = 5

Vậy S = {-2; 5}

Vậy pt là nghiệm của pt (1) nhưng ko phải nghiệm của pt (2) là 3

Vậy phương án đúng là D

Chúc bn học tốt!!

\(a)\;sinx = \frac{{\sqrt 3 }}{2}\)

Vì \(sin\frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\) nên \(sinx = \frac{{\sqrt 3 }}{2} \Leftrightarrow sin\frac{\pi }{3} = sin\frac{\pi }{3}\) \( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\\x = \pi  - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\\x = \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\)

Vậy phương trình có nghiệm là \(x = \frac{\pi }{3} + k2\pi \) hoặc \(x = \frac{{2\pi }}{3} + k2\pi \)\(,k \in \mathbb{Z}\).

\(\begin{array}{l}b)\;sin(x + {30^o}) = sin(x + {60^o})\\ \Leftrightarrow \left[ \begin{array}{l}x + {30^o} = x + {60^o} + k{360^o},k \in \mathbb{Z}\\x + {30^o} = {180^o} - x - {60^o} + k{360^o},k \in \mathbb{Z}\end{array} \right.\\ \Leftrightarrow x = {45^o} + k{180^o},k \in \mathbb{Z}.\end{array}\)

Vậy phương trình có nghiệm là \(x = {45^o} + k{180^o},k \in \mathbb{Z}\).

Đáp án D

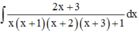
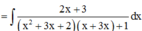
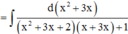
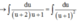
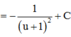
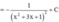
Suy ra tổng của các nghiệm của phương trình g(x) = 0 là  - 3

Đáp án D

Đặt \(\sqrt{x^2+5x+10}=a\ge0\)

\(PT\Leftrightarrow a^2+2a-8=0\\ \Leftrightarrow a=2\left(a\ge0\right)\\ \Leftrightarrow x^2+5x+10=4\\ \Leftrightarrow x^2+5x+6=0\\ \Leftrightarrow\left[{}\begin{matrix}x_1=-2\\x_2=-3\end{matrix}\right.\Leftrightarrow x_1^2+x_2^2=4+9=13\)

Vậy ...

Đặt \(\sqrt{x^2+5x+10}=t>0\Rightarrow x^2+5x=t^2-10\)

Phương trình trở thành:

\(t^2-10+2+2t=0\)

\(\Leftrightarrow t^2+2t-8=0\Rightarrow\left[{}\begin{matrix}t=2\\t=-4\left(loại\right)\end{matrix}\right.\)

\(\Rightarrow\sqrt{x^2+5x+10}=2\)

\(\Leftrightarrow x^2+5x+6=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=-3\end{matrix}\right.\)

Chọn D.

Phương trình đã cho tương đương với phương trình

z( z + 2) ( z - 1) ( z + 3)

Hay ( z² + 2z) ( z² + 2z - 3) = 10

Đặt t = z² + 2z. Khi đó phương trình trở thành: t² - 2t – 10 = 0.

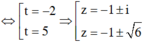
Vậy phương trình có các nghiệm: 

Tổng tất cả  các phần thực của các nghiệm phương trình đã cho là:

-1+ ( -1) + (-1) + ( -1) = -4.

\(x\left(2x-3\right)\left(x^2+10\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=0\\2x-3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{3}{2}\end{cases}}\)

Ta thấy thừa số 3 có  \(x^2+10>0\)

Vì vậy thừa số 3 không thể bằng 0 

Vậy , tổng các nghiệm thõa mãn là \(\frac{3}{2}\)

Ta có:

x(2x-3)(\(x^2\)+10)=0

\(\Leftrightarrow\)\(\hept{\begin{cases}x=0\\2x-3=0\\^{x^2+10=0}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\2x=3\\x^2=-10\left(\text{vô lý}\right)\text{ }\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=0\\x=\frac{3}{2}\end{cases}}\)

Vậy x=0;\(\frac{3}{2}\) là nghiệm của phương trình

10x²/x²-100 < 10

<=> 10x²/x²-100  - 10 <0

<=> 10x^2 - 10(x^2-100)/x^2 - 100 <0

<=> 1000/x^2-100 <0

<=> x^2 - 100 <0

<=> x^2 <100

<=> 0 <x <10

=> x nguyên dương => x= 1,2,3,...,9

=> tổng các nghiệm nguyên dương của bpt là 1+2+3+...+9=9.10/2 = 45