Cho hình vuông ABCD cạnh a. Khi đó AB → . AC → bằng:
A. a 2 .
B. a 2 2 .
C. 2 2 a 2 .
D. a 2 2 .
Cho hình vuông ABCD có cạnh bằng a. Khi đó A B → + D B → bằng:
A. a 3 3
B. a 5
C. a 3 2
D. a 5 2
Gọi H là điểm nằm trên cạnh AB sao cho B là trung điểm AH.
Ta có: AH = 2AB = 2a.
Áp dụng định lí Pytago vào tam giác ADH ta có:
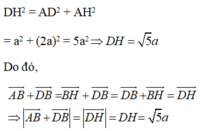
Đáp án B
Cho hình vuông ABCD có AB = 16cm, AC cắt BD tại O. Một góc vuông xOy, có tia Ox cắt cạnh AB tại E và tia Oy cắt cạnh BC tại F. Khi đó diện tích tứ giác OEBF là …cm2.
từ O hạ đường cao OH,OK ứng với AB và BC => OH=OK=8cm
có tgAOE=tgBOF (g.c.g) do
góc AOE=góc BOF (cùng phụ với xOy)
OA=OB
góc BOA= góc ABO (cùng phụ với góc ABO)
=> AE=BF
SOEBF = SEOB + SBOF = OH.EB/2 + OK.BF/2= OH( EB/2 + BF/2)= OH.((EB+AE)/2 )=(8.16)/2=64 cm2
SOEBF= SEOB + SBOF =
Cảm ơn bạn Nguyễn Đức Huy nhiều nhé.
Năm mới chúc bạn luôn mạnh khỏe, hạnh phúc và làm việc gì cũng thành công nhé.
Cho ABCD là hình vuông cạnh 4 cm (hình vẽ). Khi đó, độ dài đường chéo AC là
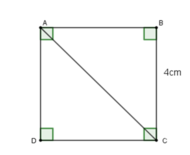
A. AC= 32 cm
B. AC=5cm
C. AC= 30 cm
D. AC=8cm
Cho hình vuông ABCD cạnh a . Tính |BC + AB| ; |AB - AC| theo a
\(\left|\overrightarrow{BC}+\overrightarrow{AB}\right|=\left|\overrightarrow{AC}\right|=AC=a\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{AB}+\overrightarrow{CA}\right|=\left|\overrightarrow{CB}\right|=CB=a\)
Hình bạn tự vẽ nha![]()
Cho hình thang cân ABCD có đáy nhỏ AB = cạnh bên BC dường chéo AC vuông góc với cạnh bên AD.
a, Tính các góc trong hình thang cân đó
Cho hình vuông ABCD cạnh a. Tính A B → + A C → + A D →
A. 3a
B. 2 + 2 a
C. a 2
2 2 a
cho hình vuông ABCD có độ dài cạnh bằn 1 dm vẽ hai đường tròn có bán kính bằng độ dài cạnh hình vuông có tâm lần lượt là A và C hãy tính diện tích còn lại
mau lên mình cho 6 like
Cho hình thang ABCD vuông tạ A và D. AB=AD=a, CD=2a. Khi đó tích vô hướng \(\overrightarrow{AC}.\overrightarrow{BD}\)
\(\overrightarrow{AC}.\overrightarrow{BD}=\left(\overrightarrow{AD}+\overrightarrow{DC}\right)\left(\overrightarrow{BA}+\overrightarrow{AD}\right)\)
\(=\overrightarrow{AD}.\overrightarrow{BA}+\overrightarrow{AD}^2+\overrightarrow{DC}.\overrightarrow{BA}+\overrightarrow{DC}.\overrightarrow{AD}\)
\(=\overrightarrow{AD}^2-\overrightarrow{AB}.\overrightarrow{DC}=a^2-a.2a=-a^2\)
Bài 1 : Hình thoi ABCD có góc B = 120 và AB = 5 cm . Khi đó độ dài đoạn BD là :
Bài 2 : Cho hình thang ABCD có cạnh = 2 cm , góc A = 60 . Khi đó độ dài đường chéo AC của hình thang là :
Bài 3 : Cho hình bình hành ABCD có góc A = 2 . góc B và AD = AB . Khi đó số đo của góc BAC là
Bai 1:
Ta co: BD la duong cheo vua la duong phan giac ( T/c cua duong cheo trong hinh thoi )
Thay co goc B = 120 cm, suy ra goc ABC = 60 do
Tam giac ABC la tam giac deu
AB = AD = BD = 5