Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số y = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên đoạn [0;2] không vượt quá 20. Tổng các phần tử của S bằng
A.210
B.-195
C.105
D.300
Gọi S là tập tất cả các giá trị nguyên của tham số thực m sao cho giá trị lớn nhất của hàm số y = 1 4 x 4 - 14 x 2 + 48 x + m - 30 trên đoạn [0;2] không vượt quá 30. Tính tổng tất cả các phần tử của S
A.108
B.120
C.210
D.136
Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số y = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên đoạn [0;2] không vượt quá 20. Tổng các phần tử của S bằng
A. 210
B. -195
C. 105
D. 300
Chọn C
Xét hàm số ![]() trên đoạn [0;2]
trên đoạn [0;2]
![]()
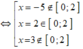
Bảng biến thiên:
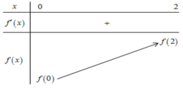
với f(0) = m - 20; f(2) = m + 6
Xét hàm số y = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên đoạn [0;2]
+ Trường hợp 1: ![]() Ta có:
Ta có:
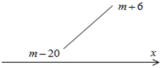
![]()
![]() suy ra không có giá trị m.
suy ra không có giá trị m.
+ Trường hợp 2: ![]() Ta có:
Ta có:

![]()
![]()
Vì m nguyên nên ![]()
+ Trường hợp 3: ![]()
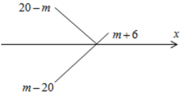
![]()
![]()
Vì m nguyên nên ![]()
Vậy ![]() Tổng các phần tử của S bằng
Tổng các phần tử của S bằng 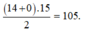
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số y = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên đoạn [0;2] không vượt quá 20. Tổng các phần tử của S bằng:
A. 210
B. 105
C. -195
D. 300
Đáp án B
Xét hàm số f x = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên [0;2] có f ' x = 0 ⇔ x = 2
Tính f 0 = m - 20 ; f 2 = m + 6 → m a x 0 ; 2 y = m a x [ 0 ; 2 ] f x = m - 20 ; m + 6
TH1. Với m a x 0 ; 2 y = m - 20 ⇒ m - 20 ≥ m + 6 m - 20 ≤ 20 ⇔ m ≤ 7 - 20 ≤ m ≤ 20 ⇔ 0 ≤ m ≤ 7
TH2. Với m a x 0 ; 2 y = m + 6 ⇒ m - 20 ≤ m + 6 m + 6 ≤ 20 ⇔ m ≥ 7 - 20 ≤ m + 6 ≤ 20 ⇔ 7 ≤ m ≤ 14
Kết hợp với m ∈ ℤ , ta được m = 0 ; 1 ; 2 ; . . . ; 14 → ∑ m = 105 .
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số y = x 2 + m x + m x + 1 trên [1;2] bằng 2. Số phần tử của S là
A. 1
B. 4
C. 3
D. 2
Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số y = x 3 − 3 x + m trên đoạn 0 ; 2 bằng 3. Số phần tử của S là:
A. 1
B. 2
C. 0
D. 6
Đáp án B.
Xét f x = x 3 − 3 x + m trên đoạn 0 ; 2
Ta có: f ' x = 3 x 3 3 = 0 ⇒ x = 1
Lại có:
f 0 = m ; f 1 = m − 2 ; f 2 = m + 2
Do đó: f x ∈ m − 2 ; m + 2
Nếu
m − 2 ≥ 0 ⇒ Max 0 ; 2 f x = m + 2 = 3 ⇔ m = 1 (loại).
Nếu m − 2 < 0 ⇒ Max 0 ; 2 f x = m + 2 Max 0 ; 2 f x = 2 − m
TH1: Max 0 ; 2 f x = m + 2 = 3 ⇔ m = 1 ⇒ 2 − m = 1 < 3 t / m
TH2: Max 0 ; 2 f x = 2 − m = 3 ⇔ m = − 1 ⇒ m + 2 = 1 < 3 t / m
Vậy m = 1 ; m = − 1 là giá trị cần tìm.
Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số y = x 3 − 3 x + m trên đoạn [0;2] bằng 3. Số phần tử của S là:
A. 1
B. 2
C. 0
D. 6
Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số y = x 3 - 3 x + m trên đoạn [0;2] bằng 3. Số phần tử của S là:
A. 1
B. 2
C. 0
D. 6
Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số y = x 2 - 3 x + m trên đoạn [ 0; 2] bằng 3. Số phần tử của S là
A. 1
B. 2
C. 3
D. 5
+ Xét hàm số f(x) = x3-3x+ m là hàm số liên tục trên đoạn [0; 2] .
Ta có đạo hàm f’ (x) = 3x2- 3 và f’ (x) = 0 khi x= 1 ( nhận ) hoặc x= -1( loại)
+ Suy ra GTLN và GTNN của f(x) thuộc { f(0); f(1) ; f(2) }={m;m-2; m+2}.
+ Xét hàm số y = x 3 - 3 x + m trên đoạn [0; 2 ] ta được giá trị lớn nhất của y là
m a x m ; m - 2 ; m + 1 = 3 .
TH1: m= 3 thì max {1;3;5}= 5 ( loại )
TH2: 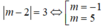
+ Với m= -1. Ta có max {1; 3}= 3 (nhận).
+Với m= 5. Ta có max { 3;5;7}= 7 (loại).
TH3: 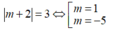
+ Với m= 1. Ta có max {1; 3}= 3 (nhận).
+ Với m= -5. Ta có max {3;5;7}= 7 (loại).
Do đó m= -1 hoặc m= 1
Vậy tập hợp S có phần tử.
Chọn B.
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số y = x 3 − 3 x + m trên đoạn [0;2] bằng 3. Tập hợp S có bao nhiêu phần tử?
A. 1
B. 2
C. 6
D. 0