Phân tích lực F → thành 2 lực F 1 → và F 2 → theo 2 phương OA và OB như hình. Cho biết độ lớn của 2 lực thành phần này
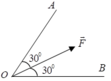
A. 1 2 F = F 1 = F 2
B. F = F 1 = F 2
C. F 1 = F 2 = 0 , 58 F
D. F 1 = F 2 = 1 , 15 F
Phân tích lực F → thành 2 lực F 1 → và F 2 → hai lực này vuông góc nhau. Biết độ lớn của F =50N; F 1 = 40 N thì độ lớn của lực F 2 là:
A. F 2 = 30 N
B. F 2 = 10 41 N
C. F 2 = 90 N
D. F 2 = 80 N
Đáp án A
Vì F 2 = F 1 2 + F 2 2
⇒ 50 2 = 40 2 + F 2 2 ⇒ F 2 = 30 N
Phân tích vecto lực F thành lực vecto lực F1 và vecto lực F2 theo hai phương OA và OB (hình 9.10). Giá trị nào sau đây là độ lớn của hai lực thành phần?
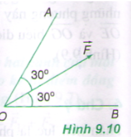
A. F1 = F2 = F
B. F1 = F2 = F/2
C. F1 = F2 = 1,15F
D. F1 = F2 = 0,58F
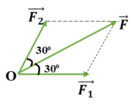
Áp dụng quy tắc hình bình hành: Từ điểm ngọn của vecto F lần lượt vẽ các đoạn song song với hai phương OA và OB ta được các vecto F1 trên OA và F2 trên OB sao cho
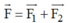
Hình bình hành có đường chéo cũng là đường phân giác của 1 góc nên nó là hình thoi.
Suy ra: F1 = F2
Mà
![]()
![]()
Phân tích lực F → thành 2 lực F 1 → v à F 2 → , hai lực này vuông góc nhau. Biết độ lớn của F =50N; F 1 = 40 N thì độ lớn của lực F 2 là:
A. F 2 = 30 N
B. F 2 = 10 41 N
C. F 2 = 90 N
D. F 2 = 80 N
Phân tích lực F → thành 2 lực F 1 → v à F 2 → theo 2 phương OA và OB như hình. Cho biết độ lớn của 2 lực thành phần này
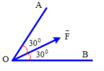
A. 1 2 F = F 1 = F 2
B. F = F 1 = F 2
C. F 1 = F 2 = 0 , 58 F
D. F 1 = F 2 = 1 , 15 F
Phân tích lực F thành hai lực thành phần F 1 và F 2 vuông góc với nhau. Biết độ lớn của lực F = 100 N; F 1 = 60 N thì độ lớn của lực F 2 là
A. 40 N.
B. 80 N.
C. 160 N.
D. 640 N.
Đáp án B
F1 và F2 là hai lực vuông góc với nhau nên ta có:

Phân tích lực F → thành hai lực F 1 → v à F 2 → , hai lực này vuông góc nhau. Biết độ lớn của lực F = 100N, F 1 = 60N thì độ lớn của lực F 2 là:
A. 80N
B. 40N
C. 160N
D. 116,6N
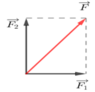
Ta có:
F 1 → ⊥ F 2 → ⇒ F 2 = F 1 2 + F 2 2 ⇒ F 2 = F 2 − F 1 2 = 100 2 − 60 2 = 80 N
Đáp án: A
Hãy dùng quy tắc hình bình hành lực và quy tắc đa giác lực để tìm hợp lực của ba lực F → 1 , F → 2 v à F → 3 có độ lớn bằng nhau và bằng 15N, cùng nằm trong một mặt phẳng. Biết rằng lực F → 2 làm thành với hai lực F → 1 v à F → 3 những góc đều là 60 ° .
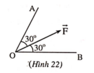
Phân tích lực F → thành hai lực F 1 → v à F 2 → theo hai phương OA và OB (Hình 22). Tìm độ lớn của hai thành phần này, biết F = 60N
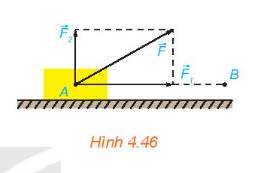
Một lực \(\overrightarrow F \) không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ A đến B. Lực \(\overrightarrow F \) được phân tích thành hai lực thành phần là \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) \((\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \;).\)
a) Dựa vào tính chất của tích vô hướng, hãy giải thích vì sao công sinh bởi lực \(\overrightarrow F \) (đã được đề cập ở trên) bằng tổng của các công sinh bởi các lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
b) Giả sử các lực thành phần \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \)tương ứng cùng phương, vuông góc với phương chuyển động của vật. Hãy tìm mối quan hệ giữa các công sinh bởi lực \(\overrightarrow F \) và lực \(\overrightarrow {{F_1}} \).
Tham khảo:
a)
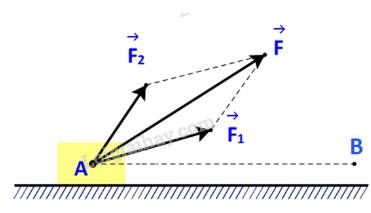
Gọi \(A,{A_1},{A_2}\) lần lượt là công sinh bởi lực \(\overrightarrow F \), \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
Ta cần chứng minh: \(A = {A_1} + {A_2}\)
Xét lực \(\overrightarrow F \), công sinh bởi lực \(\overrightarrow F \) là: \(A = \left| {\overrightarrow F } \right|.{\rm{ AB}}.\cos \left( {\overrightarrow F ,\overrightarrow {AB} } \right) = \overrightarrow F .\overrightarrow {AB} \)
Tương tự, ta có: \({A_1} = \overrightarrow {{F_1}} .\overrightarrow {AB} \), \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} \)
Áp dụng tính chất của tích vô hướng ta có:
\({A_1} + {A_2} = \overrightarrow {{F_1}} .\overrightarrow {AB} + \overrightarrow {{F_2}} .\overrightarrow {AB} = \left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right).\overrightarrow {AB} = \overrightarrow F .\overrightarrow {AB} = A\)
b)
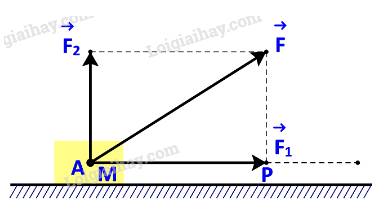
Vì \(\overrightarrow {{F_2}} \)tương ứng vuông góc với phương chuyển động nên \(\overrightarrow {{F_2}} \bot \overrightarrow {AB} \)
Do đó: công sinh bởi lực \(\overrightarrow {{F_2}} \) là: \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} = 0\)
Mà \(A = {A_1} + {A_2}\)
\( \Rightarrow A = {A_1}\)
Vậy công sinh bởi lực \(\overrightarrow F \) bằng công sinh bởi lực \(\overrightarrow {{F_1}} \).