Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD. Khi đó ( I A → + I B → ) . I D → bằng:
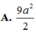
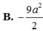
![]()
![]()
Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a. Tính D A → . B C →
A. -9a2
B. 3a2
C. 0
D. 6a2
Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD. Câu nào sau đây sai?
A. A B → . D C → = 8 a 2
B. A D → . C D → = 0
C. A D → . A B → = 0
D. D A → . D B → = 0
Chọn D.
Phương án A: ![]() = AB.DC.cos00
= AB.DC.cos00
= 8a2 nên loại A.
Phương án B: ![]() suy ra
suy ra ![]() nên loại B.
nên loại B.
Phương án C: ![]() suy ra
suy ra ![]() nên loại C.
nên loại C.
Phương án D: ![]() không vuông góc với
không vuông góc với ![]() suy ra
suy ra ![]() nên chọn D.
nên chọn D.
Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD . Khi đó I A → + I B → . I D → bằng :
A. ![]()
B. ![]()
C. 0
D. 9a2
Chọn B.
Do I là trung điểm AD nên IA = ID = 3a/2
Ta có ![]()
Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD. Khi đó I A → + I B → . I D → bằng:
A. 9 a 2 2
B. - 9 a 2 2
C. 0
D. 9 a 2
\(\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}\left(\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{AD}\right)\)
\(=\overrightarrow{AB}.\overrightarrow{CB}+\overrightarrow{AB}.\overrightarrow{BA}+\overrightarrow{AB}.\overrightarrow{AD}\)
\(=0-\overrightarrow{AB}^2+0=-4a^2\)
Cho hình thang vuông ABCD có đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = a. Gọi I là trung điểm của CD. Tìm mệnh đề đúng?
A. Góc AIB là góc vuông
B. Tam giác BIC là tam giác vuông
C. AI và BD vuông góc với nhau
D. Tất cả sai
Chọn C.
Do I là trung điểm của DC nên ta có:
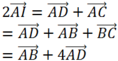
Lại có:
![]()
suy ra
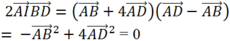
Vậy AI ⊥ BD.
Cho hình thang vuông ABCD có đường cao AB= 2a, đáy nhỏ BC=a và đáy lớn AD= 3a. Gọi M là trung điểm của CD. Chứng minh rằng BM vuông góc với AC.
cho hình thang vuông ABCD có AD=a là đường cao, đáy nhỏ AB=a, đáy lớn CD=2a. Thể tích của khối tròn xoay khi hình thang quay quanh CD là
Khi quay quanh CD sẽ tạo ra hình khối gồm 2 khối:
- Khối trụ chiều cao \(AB=a\) bán kính đáy \(r=AD=a\Rightarrow V_1=\pi.AB^2.AD^2=\pi a^3\)
- Khối nón chiều cao \(CH=\dfrac{1}{2}CD=a\) bán kính đáy \(BH=AD=a\Rightarrow V_2=\dfrac{1}{3}\pi.a^2.a=\dfrac{\pi a^3}{3}\)
\(\Rightarrow V=V_1+V_2=\pi a^3+\dfrac{\pi a^3}{3}=\dfrac{4\pi a^3}{3}\)
Cho hình thang vuông ABCD có đường cao AB=2a (a>0), đáy nhỏ AD=a, đáu lớn BC=4a. CMR: AC vuông góc BD