Cho số phức z = 1 - 1 3 i . Tìm số phức w = i z ¯ + 3 z được
A. w= 8 3
B. w= 10 3
C. w= 8 3 +i
D. w= 10 3 +i
Cho số phức z thỏa mãn z - 1 + 2 i =3 . Tìm môđun nhỏ nhất của số phức z-1 +i
A. 4
B. 2 2
C. 2
D. 2
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z ) z ¯ .
A. -2
B. 0.
C. -1
D. 1
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
![]()
![]()
![]()
![]()
Cho số phức z, biết ( 2 z - 1 ) ( 1 + i ) + ( z ¯ + 1 ) ( 1 - i ) = 2 - 2 i .
Tìm số phức liên hợp của số phức w=3z-3i
A. 1 3 - 1 3 i
B. 1 3 + 1 3 i
C. 1 - 4 i
D. 1 + 4 i
Chọn D.
Giả sử z=a+bi với a,b ∈ ℝ
Thay vào biểu thức ta được:
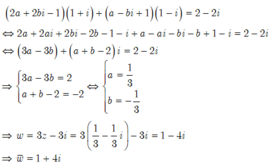
Cho hai số phức z 1 = 1 + 2 i ; z 2 = 3 - i Tìm số phức z = z 2 z 1
A. z = 1 10 + 7 10 i
B. z = 1 5 + 7 5 i
C. z = 1 5 - 7 5 i
D. z = - 1 10 + 7 10 i
Cho hai số phức z 1 = 1 + 2 i , z 2 = 3 − i . Tìm số phức z = z 2 z 1
A. z = 1 10 + 7 10 i
B. z = 1 5 + 7 5 i
C. z = 1 5 − 7 5 i
D. z = − 1 10 + 7 10 i
Đáp án C.
Ta có
z = z 2 z 1 = 3 − i 1 + 2 i = 3 − i 1 − 2 i 1 + 2 i 1 − 2 i = 1 − 7 i 5 = 1 5 − 7 5 i
Cho số phức z thỏa mãn ![]() z
(
1
-
2
i
)
+
z
¯
i
=
15
+
i
z
(
1
-
2
i
)
+
z
¯
i
=
15
+
i
Tìm môđun của số phức z.
A. z = 5
B. z = 4
C. z = 2 5
D. z = 2 3
Đáp án A
Phương pháp
Gọi ![]()
Sử dụng định nghĩa hai số phức bằng nhau.
Cách giải
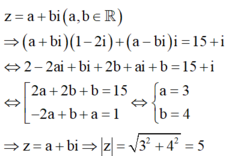
Cho số phức z thỏa mãn z(1+i)+12i=3. Tìm phần ảo của số z
A. - 9 2
B. - 15 2
C. 15 2 i
D. 15 2
Cho số phức z thỏa mãn: |z-3-2i| = 1. Tìm giá trị nhỏ nhất của | z ¯ -1-i|
A. 4
B. 5 - 1
C. 6
D. 5 + 1
Đáp án B
Gọi: ![]()
Ta có:
![]()
![]()
![]()
![]()
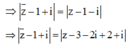
![]()
![]()
=> Giá trị nhỏ nhất của z ¯ -1-i| là 5 - 1
Cho số phức z thỏa mãn: z − 3 − 2 i = 1 . Tìm giá trị nhỏ nhất của z ¯ − 1 + i .
A. 4
B. 5 − 1
C. 6
D. 5 + 1
Đáp án B
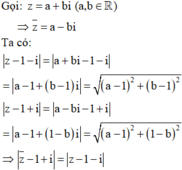
⇒ z ¯ − 1 + i = z − 3 − 2 i + 2 + i ≥ z − 3 − 2 i − 2 + i
⇒ z ¯ − 1 + i ≥ 1 − 5 = 5 − 1
=> Giá trị nhỏ nhất của z ¯ − 1 + i là 5 − 1