Với giá trị nào của tham số m để phương trình 4 x - m . 2 x + 1 + 2 m + 3 = 0 có hai nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 4
A. m = 5 2
B. m = 2
C. m = 8
D. m = 13 2
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0
với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x ∈ ( - ∞ , 0 )
A. m > 2 + 2 3 3
B. m > 2 - 2 3 3
C. m ≥ 2 - 2 3 3
D. m ≥ - 2 - 2 3 3
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0 với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho có nghiệm đúng với mọi x ∈ - ∞ ; 0
A. m ≥ 2 - 2 3 3
B. m > 2 - 2 3 3
C. m > 2 + 2 3 3
D. m ≥ - 2 - 2 3 3
Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt  , tìm điều kiện của t.
, tìm điều kiện của t.
Đưa về bất phương trình dạng ![]()
Cách giải :
![]()

Ta có 

Đặt  , khi đó phương trình trở thành
, khi đó phương trình trở thành
![]()

![]()
![]()
![]()
![]()
Ta có: 



Vậy 
Phương trình ẩn x:x+2/x-m+x-m/x-2=2
A.giải phương trình với m=1
B.tìm các giá trị của tham số m để phường trình có nghiệm x=0
Cho phương trình: ( - m 2 – m + 2)x = m + 2, với m là tham số. Giá trị của m để phương trình vô số nghiệm là:
A. m = 1
B. m = 2
C. m = -2
D. m Є {1; 2}
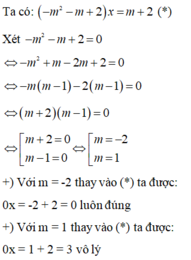
Vậy với m = -2 thì phương trình đã cho có vô số nghiệm.
Đáp án cần chọn là: C
Cho phương trình x2 – 2(m – 1)x + 2m – 5 = 0 (m là tham số)
1/ Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m
2/ Tìm các giá trị của m để phương trình có hai nghiệm trái dậu
3/ Với giá trị nào của m thì biểu thức A = x12 + x22 đạt giá trị nhỏ nhất. Tìm giá trị đó
a/ Xét pt :
\(x^2-2\left(m-1\right)+2m-5=0\)
\(\Delta'=\left(m-1\right)^2-\left(2m-5\right)=m^2-2m+1-2m+5=m^2-4m+6=\left(m-2\right)^2+2>0\forall m\)
\(\Leftrightarrow\) pt luôn có 2 nghiệm pb với mọi m
b/ Phương trình cớ 2 nghiệm trái dấu
\(\Leftrightarrow2m-5< 0\)
\(\Leftrightarrow m< \dfrac{5}{2}\)
c/ Theo định lí Vi - et ta có :
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1.x_2=2m-5\end{matrix}\right.\)
\(A=x_1^2+x_2^2\)
\(=\left(x_1+x_2\right)^2-2x_1.x_2\)
\(=4\left(m-1\right)^2-2\left(2m-5\right)\)
\(=4m^2-8m+4-4m+10\)
\(=4m^2-12m+14=4\left(m^2-3m+\dfrac{9}{4}\right)+5=4\left(m-\dfrac{3}{2}\right)^2+5\ge5\)
\(A_{min}=5\Leftrightarrow m=\dfrac{3}{2}\)
1, \(\Delta'=\left(m-1\right)^2-\left(2m-5\right)=m^2-4m+6=\left(m-2\right)^2+2>0\)
Vậy pt luôn có 2 nghiệm pb với mọi m
2, Vì pt có 2 nghiệm trái dấu
\(x_1x_2=\dfrac{c}{a}=2m-5< 0\Leftrightarrow m< \dfrac{5}{2}\)
3, Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=2m-5\end{matrix}\right.\)
\(A=\left(x_1+x_2\right)^2-2x_1x_2=4\left(m-1\right)^2-2\left(2m-5\right)\)
\(=4m^2-12m+14=4m^2-2.2m.3+9+6\)
\(=\left(2m-3\right)^2+6\ge6\forall m\)
Dấu ''='' xảy ra khi m = 3/2
Vậy với m = 3/2 thì A đạt GTNN tại 6
1: \(\text{Δ}=\left(2m-2\right)^2-4\left(2m-5\right)\)
\(=4m^2-8m+4-8m+20\)
\(=4m^2-16m+24\)
\(=4m^2-16m+16+8\)
\(=\left(2m-4\right)^2+8>0\forall m\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
2: Để phương trình có hai nghiệm trái dấu thì 2m-5<0
hay m<5/2
3: \(A=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(2m-2\right)^2-2\left(2m-5\right)\)
\(=4m^2-8m+4-4m+10\)
\(=4m^2-12m+14\)
\(=4m^2-12m+9+5\)
\(=\left(2m-3\right)^2+5\ge5\forall m\)
Dấu '=' xảy ra khi m=3/2
Với giá trị nào của tham số m thì phương trình x + 4 − x 2 = m có nghiệm?
A. − 2 < m < 2
B. − 2 < m < 2 2
C. − 2 ≤ m ≤ 2 2
D. − 2 ≤ m ≤ 2
Đáp án C
Ta có: x + 4 − x 2 ≤ 1 2 + 1 2 x 2 + 4 − x 2 = 8
⇒ − 2 2 ≤ x + 4 − x 2 ≤ 2 2 ⇒ để phương trình có nghiệm thì − 2 2 ≤ m ≤ 2 2 .
Cho phương trình m. sin x + 4. cos x = 2m - 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm?
A. 4
B. 7.
C. 6.
D. 5
Cho phương trình 2 x + m = 3 x − 2 . Tìm giá trị của tham số m để phương trình có nghiệm x = 4.
Thay x = 4 vào phương trình ta có: ![]()
Từ đó tìm được ![]()
Cho phương trình (2m−5)x2 −2(m−1)x+3=0 (1); với m là tham số thực
1) Tìm m để phương trình (1) có một nghiệm bằng 2, tìm nghiệm còn lại.
3) Tìm giá trị của m để phương trình đã cho có nghiệm
4) Xác định các giá trị nguyên của để phương trình đã cho có hai nghiệm phân biệt đều nguyên dương
1) điều kiện của m: m khác 5/2
thế x=2 vào pt1 ta đc:
(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)
lập △'=[-(m-1)]2-*(2m-5)*3 = (m-4)2
vì (m-4)2 ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2
3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m
Câu 2 . Cho phương trình: x’ – 2(m-1)x – 2m+1=0 (m là tham số). a) Giải phương trình với m=4 b) Tìm các giá trị của m để phương trình có hai nghiệm x và y thỏa mãn 2x, +3x=-11 cứu tuii:((
a: Khi m=4 thì (1) sẽ là:
x^2-6x-7=0
=>x=7 hoặc x=-1
b: Sửa đề: 2x1+3x2=-11
x1+x2=2m-2
=>2x1+3x2=-11 và 2x1+2x2=4m-4
=>x2=-11-4m+4=-4m-7 và x1=2m-2+4m+7=6m+5
x1*x2=-2m+1
=>-24m^2-20m-42m-35+2m-1=0
=>-24m^2-60m-34=0
=>\(m=\dfrac{-15\pm\sqrt{21}}{12}\)