Có bao nhiêu số nguyên dương n sao cho S = 2 + C 1 0 + C 2 0 + . . . + C n 0 + C 1 1 + C 2 1 + . . . + C n 1 + . . . + C n - 1 n - 1 + C n n - 1 + C n n là một số có 1000 chữ số.
A. 3
B. 1
C. 0
D. 2
Có bao nhiêu số nguyên dương n sao cho
S = 2 + C 1 0 + C 2 0 + . . . + C n 0 + C 1 1 + C 2 1 + . . . + C n 1 + . . . + C n - 1 n - 1 + C n n - 1 + C n n
là một số có 1000 chữ số
A. 2.
B. 1.
C. 3.
D. 0.
Chọn đáp án C
Ta có
S = 2 + C 1 0 + C 2 0 + . . . + C n 0 + C 1 1 + C 2 1 + . . . + C n 1 + . . . + C n - 1 n - 1 + C n n - 1 + C n n
Xét khai triển
![]()
Thay x = 1 vào khai triển ta được
![]()
Suy ra
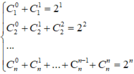
⇒ S = 2 + 2 1 1 - 2 n 1 - 2 = 2 n + 1
Số chữ số của S là
![]()
![]()
![]()
![]()
![]()
Do n ∈ Z nên n ∈ 3318 ; 3319 ; 3320 .
Vậy có 3 số nguyên dương n thỏa mãn yêu cầu bài toán
Gọi S(n) là tổng tất cả các chữ số của số nguyên dương n khi biểu diễn nó trong hệ thập phân. Biết rằng với mọi số nguyên dương n thì ta có 0<S(n)<=n. Tìm số nguyên dương n sao cho S(n)=n^2- 2011n+ 2010
\(^∗\)Xét \(n=2011\)thì \(S\left(2011\right)=2011^2-2011.2011+2010=2010\)(vô lí)
\(^∗\)Xét \(n>2011\)thì \(n-2011>0\)do đó \(S\left(n\right)=n\left(n-2011\right)+2010>n\left(n-2011\right)>n\)(vô lí do \(S\left(n\right)\le n\))
* Xét \(1\le n\le2010\)thì \(\left(n-1\right)\left(n-2010\right)\le0\Leftrightarrow n^2-2011n+2010\le0\)hay \(S\left(n\right)\le0\)(vô lí do \(S\left(n\right)>0\))
Vậy không tồn tại số nguyên dương n thỏa mãn đề bài
- Vì N là số tự nhiên có hai chữ số nên đặt \(N=\overline{ab}\) \(\left(0< a\le9;0\le b\le9;a,b\in N\right)\)
Ta có \(S\left(N\right)=S\left(\overline{ab}\right)=ab\) ; \(P\left(N\right)=P\left(\overline{ab}\right)=a+b\)
Vì \(N=S\left(N\right)+P\left(N\right)\) nên \(\overline{ab}=ab+a+b\)
\(\Rightarrow10a+b=ab+a+b\)
\(\Rightarrow9a=ab\Rightarrow b=9\) (vì a khác 0)
Vậy chữ số hàng đơn vị của N là 9 ---> chọn E
Có bao nhiêu số nguyên dương n thỏa mãn các điều kiện sau:
i) 219 ≤ n ≤ 2019
ii) Tồn tại x, y ∈ N sao cho 1 ≤ x< n< y và y chia hết cho các số nguyên dương từ 1→ n, trừ 2 số x và x+1
Với mỗi số nguyên dương n, ta kí hiệu d(n) là số các ước nguyên dương của n và s(n) là tổng tất cả các ước nguyên dương đó. Ví dụ, d(2018) = 4 vì 2018 có (và chỉ có) 4 ước nguyên dương là 1; 2; 1009; 2018 và s(2018) = 1 + 2 + 1009 + 2018 = 3030. Tìm tất cả các số nguyên dương x sao cho s(x) . d(x) = 96
1. Tìm giá trị nhỏ nhất của biểu thức: A= \(|x-3|+|x+1|\)với x \(\in\)\(ℤ\).
2. Ký hiệu S(a) là số các chữ số của số tự nhiên a. Tìm số nguyên dương n để S(5n) - S(2n) là số chẵn.
3. Tìm bộ ba số nguyên dương (a, b, c) sao cho \(\frac{1}{a}+\frac{1}{a+b}+\frac{1}{a+b+c}=1\).
4. Tích của 5 số nguyên dương là 3003. Hỏi tổng của chúng có thể nhận bao nhiêu giá trị khác nhau?
5. Chứng minh rằng trong 27 số tự nhiên tùy ý luôn tồn tại 2 số sao cho tổng hoặc hiệu của chúng chia hết cho 50.
Ai làm đúng mình tick cho!
Làm ơn có ai làm giúp mình đi! Một bài thôi cũng được.
Này m đk lm đề này ak , t bh mới đk cô cho lm . Mẹ khó vãi , mỗi câu đầu m hỏi t làm đk thôi
với mỗi số nguyên dương n, ta kí hiệu d(n) là số các ước nguyên dương của n và s(n) là tổng tất cả các ước nguyên dương đó .Chẳng hạn d(2018) = 4 vì 2018 có và chỉ có 4 ước Nguyên Dương là 1;2;1009; 2018 và s (2018) = 1 + 2 + 1009 + 2018 = 3030 Tìm tất cả các số nguyên dương x sao cho s(x).d(x)= 96
Vào đây tham khảo nha ! : Câu hỏi của Phạm Chí Cường - Toán lớp 6 | Học trực tuyến
tìm n nguyên dương sao cho s(n)=1.2.3.....7 +n(n+1)(n+2).....(n+7) có thể viết dưới dạng tổng các bình phương 2 số nguyên dương
Có bao nhiêu số nguyên dương n sao cho ![]()
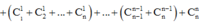 là một số có 1000 chữ số
là một số có 1000 chữ số
A. 3
B. 1
C. 0
D. 2
Đáp án A
Phương pháp :
+) Nhóm các tổ hợp có chỉ số dưới bằng nhau.
+) Sử dụng tổng 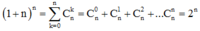
+) Sử dụng công thức tính tổng của cấp số nhân.
+) Để S là số có 1000 chữ số thì ![]()
Cách giải:
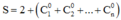
![]()
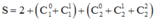
![]()
Xét tổng 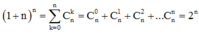
Từ đó ta có: ![]()
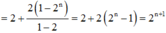
Để S là số có 1000 chữ số thì
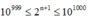
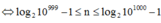
![]()
n là số nguyên dương ![]()