Cho hàm số f(x) liên tục trên R đồng thời thỏa mãn điều kiện f(-x)+2f(x)=cosx. Tính tích phân I = ∫ - π 2 π 2 f ( x ) d x
A. I = 2 3
B. I = 4 3
C. I = 1 3
D. I = 1
Cho hàm số f(x) liên tục trên R đồng thời thỏa mãn điều kiện f(-x)+2f(x)=cosx. Tính tích phân ∫ - π 2 π z f ( x ) d x
A. I= 2 3
B. I= 4 3
C. I= 1 3
D. I=1
Cho hàm số f(x) liên tục trên R và thỏa mãn f(-x)+2f(x)=cosx. Tính tích phân I = ∫ − π 2 π 2 f x d x
A. I = 4 3
B. I = 1 3
C. I = 2 3
D. I = 1
Cho hàm số f(x) liên tục trên R và thỏa mãn f(-x) + 2f(x) = cosx. Tính tích phân I = ∫ - π 2 π 2 f ( x ) d x
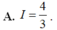
![]()
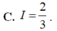
![]()
Cho hàm số f(x) liên tục trên R và thỏa mãn f(-x) + 2f(x) = cosx. Tính tích phân I = ∫ - π 2 π 2 f ( x ) d x
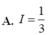
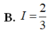
![]()
![]()
Cho hàm số f(x) liên tục trên R và thỏa mãn f - x + 2 f x = cos x . Tính tích phân I = ∫ - π 2 π 2 f x d x
A. I = 1 3
B. I = 2 3
C. I = π
D. I = 2 π
Xét tích phân J = ∫ - π 2 π 2 f - x d x
Đặt: x = -t nên dx = -dt
Đổi cận
x = = - π 2 ⇒ t = π 2 x = π 2 ⇒ t = - π 2
Khi đó
I = ∫ - π 2 π 2 f - t d t = J ⇒ 3 I + 2 I = ∫ - π 2 π 2 f - x + 2 f x d x = ∫ - π 2 π 2 cos x d x = 2
Vậy I = 2 3
Đáp án B
Cho hàm số f(x) liên tục trên R và thỏa mãn f − x + 2 f x = cos x . Tính tích phân I = ∫ − π 2 π 2 f x d x
A. I = 4 3
B. I = 1 3
C. I = 2 3
D. I = 1
Đáp án C
Cách 1: Thay x bởi -x ta được f x + 2 f − x = cos − x = cos x . Kết hợp với giả thiết ta có
f − x + 2 f x = f x + 2 f − x ⇔ f x = f − x
Suy ra f x = 1 3 cos x . Vậy I = ∫ − π 2 π 2 f x d x = 1 3 ∫ − π 2 π 2 cos x d x = 2 3 .
Cách 2: Từ giả thiết ta có ∫ − π 2 π 2 f − x + 2 f x d x = ∫ − π 2 π 2 cos x d x
⇔ ∫ − π 2 π 2 f − x d x + 2 ∫ − π 2 π 2 f x d x = 2 ⇔ ∫ − π 2 π 2 f t d t + 2 ∫ − π 2 π 2 f x d x = 2 ⇔ ∫ − π 2 π 2 f x d x = 2 3 .
Cho hàm số f(x) liên tục trên R và thỏa mãn f - x + 2 f x = cos x . Tính tích phân I = ∫ - π 2 π 2 f x d x
A. I = 1 3
B. I = 2 3
C. I = π
D. I = 2 π
Xét tích phân I = ∫ - π 2 π 2 f x d x
Đặt x = -t nên dx = -dt
Đổi cận x = - π 2 ⇒ t = π 2 ; x = π 2 ⇒ t = - π 2
Khi đó
I = ∫ - π 2 π 2 f - t d t = J ⇒ 3 I = J + 2 I = ∫ - π 2 π 2 f - x + 2 f x d x = J = ∫ - π 2 π 2 cos x d x = 2
Vậy I = 2 3
Đáp án B
Cho biết y=f(x) là hàm số liên tục và xác định trên R|{1;3} và thỏa mãn đồng thời các điều kiện: f ' ( x ) = 1 ( x - 1 ) ( x - 3 ) ; f ( 0 ) = 2 f ( 2 ) = 4 f ( 4 ) = 4 Khi đó giá trị của biểu thức: f ( - 1 ) + f 3 2 + f 9 2 nằm trong khoảng?
A . 5 - 1 2 ln 7 18
B . 7 - 1 2 ln 7 18
C . 2 + 1 2 ln 7 18
D . 3 + 1 2 ln 7 18
Cho f, g là hai hàm liên tục trên [1;3] thỏa mãn điều kiện ∫ 1 3 f ( x ) + 3 g ( x ) d x = 10 đồng thời ∫ 1 3 ( 2 f ( x ) - g ( x ) d x = 6 . Tính ∫ 1 3 f ( x ) + g ( x ) d x .
![]()
![]()
![]()
![]()