Cho lăng trụ ABC.A'B'C' có các mặt bên là hình vuông cạnh a. Gọị D,E lần lượt là trung điểm các cạnh BC, A'C'. Tính khoảng cách giữa hai đường thẳng AB' và DE theo a
A . a 3 3
B . a 3 4
C . a 3 2
D . a 3
Cho lăng trụ ABCA'B'C' có các mặt bên là hình vuông cạnh a. Gọị D,E lần lượt là trung điểm các cạnh BC,A'C' Tính khoảng cách giữa hai đường thẳng AB' ;DE theo a
A. a 3 3
B. a 3 4
C. a 3 2
D. a 3
Cho hình lăng trụ ABC.A'B'C' có các mặt bên đều là hình vuông cạnh a Gọi D,E,F lần lượt là trung điểm của các cạnh BC, A'C' , C'B' Tính khoảng cách giữa hai đường thẳng DE và AB'.
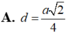
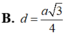
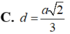
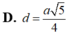
Cho hình lăng trụ A B C . A ' B ' C ' có các mặt bên đều là hình vuông cạnh a Gọi D;E;F lần lượt là trung điểm của các cạnh B C , A ' C ' , C ' B ' . Tính khoảng cách giữa hai đường thẳng DEvà AB'.
A. d = a 2 4
B. d = a 3 4
C. d = a 2 3
D. d = a 5 4
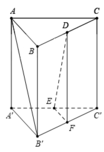
Đáp án B
Vơi D, E, F lần lượt là trung điểm của cạnh B C , A ' C ' , C ' B '
Hai mặt phẳng A B B ' A ' và D E F song song với nhau
d D E ; A B ' = d E ; A B B ' A ' = 1 2 d C ; A B B ' A ' = 1 2 . a 3 2 = a 3 4
Vậy khoảng cách cần tìm là d = α 3 4
Cho lăng trụ ABC.A'B'C' có đáy là tam tác đều cạnh a. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) là trung điểm của cạnh AB, góc giữa đường thẳng A'C và mặt phẳng đáy bằng 60 độ. Tính theo a thể tích của khối lăng trụ ABC.A'B'C' và khoảng cách từ điểm B đến mặt phẳn (ACC'A')
Gọi H là trung điểm của AB, \(A'H\perp\left(ABC\right)\) và \(\widehat{A'CH}=60^0\)
Do đó \(A'H=CH.\tan\widehat{A'CH}=\frac{3a}{2}\)
Do đó thể tích khối lăng trụ là \(V_{ABC.A'B'C'}=\frac{3\sqrt{3}a^3}{8}\)
Gọi I là hình chiếu vuông góc của H lên AC; K là hình chiếu vuông góc của H lên A'I. Suy ra :
\(HK=d\left(H,\left(ACC'A'\right)\right)\)
Ta có :
\(HI=AH.\sin\widehat{IAH}=\frac{\sqrt{3}a}{4}\);
\(\frac{1}{HK^2}=\frac{1}{HI^2}+\frac{1}{HA'^2}=\frac{52}{9a^2}\)
=>\(HK=\frac{3\sqrt{13}a}{26}\)
Do đó \(d\left(B;\left(ACC'A'\right)\right)=2d\left(H;\left(ACC'A'\right)\right)=2HK=\frac{3\sqrt{13}a}{13}\)
Cho lăng trụ \(ABC.A_1B_1C_1\) có các mặt bên là các hình vuông cạnh a. Gọi D, E, F lần lượt là các trung điểm của các cạnh \(BC,A_1C_1,B_1C_1\). Tính theo a khoảng cách giữa 2 đường thẳng \(DE,A_1F\)
Gọi (\(\alpha\)) là mặt phẳng chứa DE và song song với \(A_1F\) thì khoảng cách cần tính bằng khoảng cách từ F đến ( \(\alpha\))
Theo giả thiết suy ra lăng trụ đã cho là lăng trụ đứng có đáy là tam giác đều cạnh a
Gọi K là trung điểm của \(FC_1\) thì \(EK\)//\(A_1F\)//AD, suy ra (\(\alpha\)) \(\equiv\left(ADKE\right)\)
Ta có \(A_1F\perp B_1C_1\Rightarrow A_1F\perp\left(BCC_1B_1\right)\) \(\Rightarrow EK\perp\left(BCC_1B_1\right)\)
Gọi H là hình chiếu vuông góc của F lên đường thẳng DK thì \(FH\perp\left(ADKE\right)\) suy ra FH là khoảng cách cần tính
Trong tam giác vuông DKF, ta có :
\(\frac{1}{FH^2}=\frac{1}{FD^2}+\frac{1}{FK^2}=\frac{1}{\left(\frac{a}{4}\right)^2}\Rightarrow FH=\frac{a}{\sqrt{17}}\)
Cho lăng trụ ABC.A'B'C' có các mặt bên đều là hình vuông cạnh a. Khoảng cách giữa hai đường thẳng A’B và B’C’ bằng
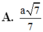
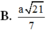
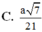
Cho lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác vuông, AB=BC=a, cạnh bên \(AA'=a\sqrt{2}\). Gọi M là trung điểm cạnh BC. Tính theo a thể tích của khối lăng trụ ABC.A'B'C' và khoảng cách giữa 2 đường thẳng AM, B'C
Từ giả thiết ta suy ra tam giác ABC là tam giác vuông cân tại B
Thể tích của khối lăng trụ là \(V_{ABC.A'B'C'}=AA'.BC=a\sqrt{2.}\frac{1}{2}a^2=\frac{\sqrt{2}}{2}a^3\)
Gọi E là trung điểm của BB'. Khi đó mặt phẳng (AME) song song với B'C nên khoảng cách giữa 2 đường thẳng AM, B'C bằng khoảng cách giữa B'C và mặt phẳng (AME)
Nhận thấy, khoảng cách từ B đến mặt phẳng (AME) bằng khoảng cách từ C đến mặt phẳng (AME)
Gọi h là khoảng cách từ B đến mặt phẳng (AME). Do đó tứ diện BAME có BA, BM, BE đôi một vuông góc với nhau nên :
\(\frac{1}{h^2}=\frac{1}{BA^2}+\frac{1}{BM^2}+\frac{1}{BE^2}\Rightarrow\frac{1}{h^2}=\frac{1}{a^2}+\frac{4}{a^2}+\frac{2}{a^2}=\frac{7}{a^2}\)
\(\Rightarrow h=\frac{a\sqrt{7}}{7}\)
Vậy khoảng cách giữa 2 đường thẳng B'C và AM bằng \(\frac{a\sqrt{7}}{7}\)
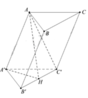
Cho hình lăng trụ ABC.A'B'C' có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30 0 . Hình chiếu H của A trên mặt phẳng (A'B'C') là trung điểm của B’C’. Tính theo a khoảng cách giữa hai mặt phẳng đáy của lăng trụ ABC.A'B'C'.
![]()
![]()

Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a.hình chiếu vuông góc của A' trên mặt phẳng (ABC) là trung điểm của cạnh AB, góc giữa A'C và mặt phẳng đáy là 60°.tính theo a thể tính hình lăng trụ và khoảng từ B đến mặt phẳng (ACA'C')