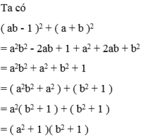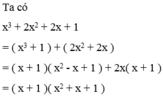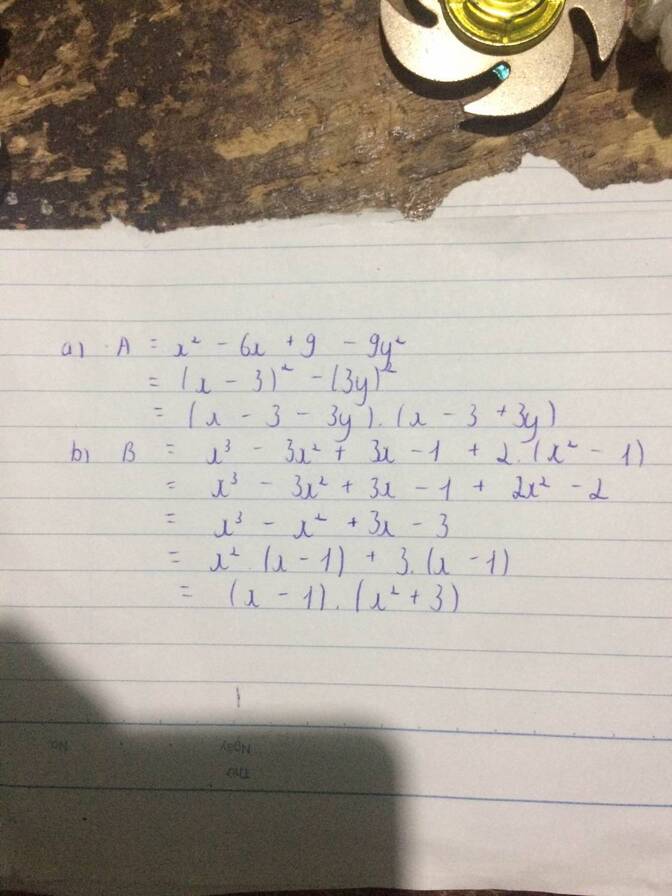\(1,\\ 1,=15\left(x+y\right)\\ 2,=4\left(2x-3y\right)\\ 3,=x\left(y-1\right)\\ 4,=2x\left(2x-3\right)\\ 2,\\ 1,=\left(x+y\right)\left(2-5a\right)\\ 2,=\left(x-5\right)\left(a^2-3\right)\\ 3,=\left(a-b\right)\left(4x+6xy\right)=2x\left(2+3y\right)\left(a-b\right)\\ 4,=\left(x-1\right)\left(3x+5\right)\\ 3,\\ A=13\left(87+12+1\right)=13\cdot100=1300\\ B=\left(x-3\right)\left(2x+y\right)=\left(13-3\right)\left(26+4\right)=10\cdot30=300\\ 4,\\ 1,\Rightarrow\left(x-5\right)\left(x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\\ 2,\Rightarrow\left(x-7\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ 3,\Rightarrow\left(3x-1\right)\left(x-4\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=4\end{matrix}\right.\\ 4,\Rightarrow\left(2x+3\right)\left(2x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)

a) Ta thấy đa thức \(f\left(x\right)=4x^2+81\) vô nghiệm (*).

 Giả sử \(f\left(x\right)\) có thể phân tích được thành nhân tử, khi đó \(f\left(x\right)=\left(ax+b\right)\left(cx+d\right)\), suy ra \(f\) có nghiệm là \(x=-\dfrac{b}{a}\) hoặc \(x=-\dfrac{d}{c}\), mâu thuẫn với (*).

 Vậy ta không thể phân tích \(f\left(x\right)\) thành nhân tử.

b) \(g\left(x\right)=x^7+x^2+1\)

\(g\left(x\right)=x^7-x+x^2+x+1\)

\(g\left(x\right)=x\left(x^6-1\right)+\left(x^2+x+1\right)\)

\(g\left(x\right)=x\left(x^3-1\right)\left(x^3+1\right)+\left(x^2+x+1\right)\)

\(g\left(x\right)=x\left(x^3+1\right)\left(x-1\right)\left(x^2+x+1\right)+\left(x^2+x+1\right)\)

\(g\left(x\right)=\left(x^2+x+1\right)\left(x^5-x^4+x^2-x+1\right)\)

 Xét \(h\left(x\right)=x^5-x^4+x^2-x+1\), nếu \(h\left(x\right)\) phân tích được thành nhân tử thì nó có nghiệm hữu tỉ. Khi đó nó có dạng \(x=\dfrac{p}{q},\left(p,q\inℤ;\left(p,q\right)=1\right),p|1,q|1\) \(\Rightarrow x=\pm1\). Ta thấy \(h\left(1\right).h\left(-1\right)\ne0\) nên 2 nghiệm này không thỏa mãn. Vậy h(x) không có nghiệm hữu tỉ \(\Rightarrow\) g(x) không thể phân tích tiếp.

a)

\(4x^2+81\\=(2x)^2+2\cdot2x\cdot9+9^2-36x\\=(2x+9)^2-36x\)

Bạn xem lại đề bài nhé!

b)

\(x^7+x^2+1\\=(x^7+x^6+x^5)-x^6-x^5-x^4+(x^4+x^3+x^2)-(x^3-1)\\=x^5(x^2+x+1)-x^4(x^2+x+1)+x^2(x^2+x+1)-(x-1)(x^2+x+1)\\=(x^2+x+1)(x^4-x^4+x^2-x+1)\)

a) \(A=x^2-6x+9-9y^2\)

\(=\left(x-3\right)^2-\left(3y\right)^2\)

\(=\left(x-3-3y\right)\left(x-3+3y\right)\)

b) \(B=x^3-3x^2+3x-1+2\left(x^2-1\right)\)

\(=\left(x-1\right)^3+\left(2x+2\right)\left(x-1\right)\)

\(=\left(x-1\right)\left[\left(x-1\right)^2+2x+2\right]\)

\(=\left(x-1\right).\left(x^2+3\right)\)

a, \(A=\left(x-3\right)^2-9y^2=\left(x-3-3y\right)\left(x-3+3y\right)\)

b, \(B=\left(x-1\right)^3+2\left(x-1\right)\left(x+1\right)=\left(x-1\right)\left[\left(x-1\right)^2+2\left(x+1\right)\right]\)

\(=\left(x-1\right)\left(x^2-2x+1+2x+2\right)=\left(x-1\right)\left(x^2+3\right)\)

\(2ab^2-a^2b-b^3=b^2\left(2a-a^2-b\right)\)

\(2ab^2-a^2b-b^3\)

\(=-b\left(a^2-2ab+b^2\right)\)

\(=-b\left(a-b\right)^2\)

-(2ab² - a²b - b³)

= b(-2ab + a² + b²)

= b(a² - 2ab + b²)

= b(a - b)²

a) \(10x^2+10xy-x-y=10x\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(10x-1\right)\)

Bài 1: 

a: \(4a^2-6b=2\left(2a^2-3b\right)\)

b: \(m^3n-2m^2n^2-mn\)

\(=mn\left(m^2-2mn-1\right)\)

Bài 1:

a) \(4a^2-6b=2\left(a^2-3b\right)\)

b) \(=mn\left(m^2-2mn-1\right)\)

Bài 2:

a) \(=4\left(u-2\right)^2+v\left(u-2\right)=\left(u-2\right)\left(4u-8+v\right)\)

b) \(=a\left(a-b\right)^3-b\left(a-b\right)^2-b^2\left(a-b\right)=\left(a-b\right)\left[a\left(a-b\right)^2-b\left(a-b\right)-b^2\right]=\left(a-b\right)\left(a^3-2a^2b+ab^2-ab+b^2-b^2\right)=\left(a-b\right)\left(a^3-2a^2b+ab^2-ab\right)\)

Bài 4: 

Ta có: \(\left(x^3-x^2\right)-4x^2+8x-4=0\)

\(\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\)

\(\Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)