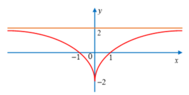
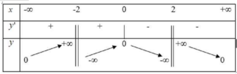
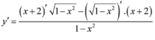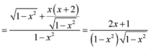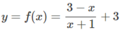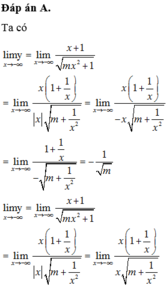Cho hàm số y = x + 2 1 - x 2 . Xét các mệnh đề sau đây:
(I). Hàm số có tập xác định D=(-1;1).
(II). Đồ thị hàm số có 2 đường tiệm cận ngang là y=1 và y=-1.
(III). Đồ thị hàm số có 2 đường tiệm cận đứng là x=1 và x=-1.
(IV). Hàm số có một cực trị.
Số mệnh đề đúng là:
A.3
B.1
C.2
D.4