tìm x , y
3xy-3x+y=0
tìm x; y
3xy-x+y=5
\(x\left(3y-1\right)+y=5\)
\(3x\left(3y-1\right)+3y=15\)
\(3x\left(3y-1\right)+3y-1=14\)
\(\left(3x-1\right)\left(3y-1\right)=14\)
Đến đây đưa về phương trình ước số
3xy-x+y=5
Ta tính:3xy-x+y=5
Ta có :
\(3\times x-x+y-x+y=5\) (ta chuyển xy thành x-y)
\(\Rightarrow3-1x=5\)
x =3-5
x=-2
Vậy x=-2
Ta tính:\(3\times-2y=5\)
Sau khi ta có x=-2 thì:
\(-2y=3-5\)
\(-2y=-2\)
\(y=-2\div-2\)
\(y=1\)
Vậy y=1
Suy ra x=-2 và y=1
Cho hai số thực x,y thỏa mãn: 9 x 3 + ( 2 - y 3 x y - 5 ) x + 3 x y - 5 = 0 . Tìm giá trị nhỏ nhất của P = x 3 + y 3 + 6 x y + 3 ( 3 x 2 + 1 ) ( x + y - 2 )
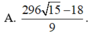
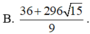
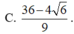
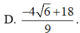
Bài 1: Tìm x € Z a)1−3x chia hết cho x−2 b)3x+2 chia hết cho 2x+1 Bài 2: Tìm các số nguyên a)x(3−y)−y=0 b)xy+2x+2y=0 c)xy−2x+4y=1 d)x(y+1)+y=0
Bài 1:a) Ta có: \(1-3x⋮x-2\)
\(\Leftrightarrow-3x+1⋮x-2\)
\(\Leftrightarrow-3x+6-5⋮x-2\)
mà \(-3x+6⋮x-2\)
nên \(-5⋮x-2\)
\(\Leftrightarrow x-2\inƯ\left(-5\right)\)
\(\Leftrightarrow x-2\in\left\{1;-1;5;-5\right\}\)
hay \(x\in\left\{3;1;7;-3\right\}\)
Vậy: \(x\in\left\{3;1;7;-3\right\}\)
b) Ta có: \(3x+2⋮2x+1\)
\(\Leftrightarrow2\left(3x+2\right)⋮2x+1\)
\(\Leftrightarrow6x+4⋮2x+1\)
\(\Leftrightarrow6x+3+1⋮2x+1\)
mà \(6x+3⋮2x+1\)
nên \(1⋮2x+1\)
\(\Leftrightarrow2x+1\inƯ\left(1\right)\)
\(\Leftrightarrow2x+1\in\left\{1;-1\right\}\)
\(\Leftrightarrow2x\in\left\{0;-2\right\}\)
hay \(x\in\left\{0;-1\right\}\)
Vậy: \(x\in\left\{0;-1\right\}\)
Bài 1 :
a, Có : \(1-3x⋮x-2\)
\(\Rightarrow-3x+6-5⋮x-2\)
\(\Rightarrow-3\left(x-2\right)-5⋮x-2\)
- Thấy -3 ( x - 2 ) chia hết cho x - 2
\(\Rightarrow-5⋮x-2\)
- Để thỏa mãn yc đề bài thì : \(x-2\inƯ_{\left(-5\right)}\)
\(\Leftrightarrow x-2\in\left\{1;-1;5;-5\right\}\)
\(\Leftrightarrow x\in\left\{3;1;7;-3\right\}\)
Vậy ...
b, Có : \(3x+2⋮2x+1\)
\(\Leftrightarrow3x+1,5+0,5⋮2x+1\)
\(\Leftrightarrow1,5\left(2x+1\right)+0,5⋮2x+1\)
- Thấy 1,5 ( 2x +1 ) chia hết cho 2x+1
\(\Rightarrow1⋮2x+1\)
- Để thỏa mãn yc đề bài thì : \(2x+1\inƯ_{\left(1\right)}\)
\(\Leftrightarrow2x+1\in\left\{1;-1\right\}\)
\(\Leftrightarrow x\in\left\{0;-1\right\}\)
Vậy ...
Tìm x, y biết
a,/2x/+/y-3/=0
b,/3x-6/+/3x-y+5/=0
c,34-2./9-3x/=0
Bài 1:a)Tìm x biết |3x-12|+4x=2x-2 b)tìm x,y biết |6+x|+(3+y)2=0
Bài 2:Tìm x để g(x)=0 biết rằng g(x)=3x2-3-8g(x)
b
\(\left|6+x\right|\ge0;\left(3+y\right)^2\ge0\Rightarrow\left|6+x\right|+\left(3+y\right)^2\ge0\)
Suy ra \(\left|6+x\right|+\left(3+y\right)^2=0\)\(\Leftrightarrow\hept{\begin{cases}6+x=0\\3+y=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-6\\y=-3\end{cases}}\)
a
Ta có:\(\left|3x-12\right|=3x-12\Leftrightarrow3x-12\ge0\Leftrightarrow3x\ge12\Leftrightarrow x\ge4\)
\(\left|3x-12\right|=12-3x\Leftrightarrow3x-12< 0\Leftrightarrow3x< 12\Leftrightarrow x< 4\)
Với \(x\ge4\) ta có:
\(3x-12+4x=2x-2\)
\(\Rightarrow5x=10\)
\(\Rightarrow x=2\left(KTMĐK\right)\)
Với \(x< 4\) ta có:
\(12-3x+4x=2x-2\)
\(\Rightarrow10=x\left(KTMĐK\right)\)
Câu 1:
A = (3 - y)(4 - x)(2y + 3x)
6A = (6 - 2y)(12 - 3x)(2y + 3x)
Ta có: \(\hept{\begin{cases}0\le x\le4\\0\le y\le3\end{cases}\Leftrightarrow\hept{\begin{cases}4-x\ge0\\3-y\ge0\\2y+3x\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}12-3x\ge0\\6-2y\ge0\\2y+3x\ge0\end{cases}}}\)
Áp dụng BĐT cô-si ta được:
\(\left(12-3x\right)+\left(6-2y\right)+\left(2y+3x\right)\ge3.\sqrt[3]{\left(12-3x\right)\left(6-2y\right)\left(2y+3x\right)} \)
\(\Leftrightarrow3.\sqrt[3]{6A}\le18\Leftrightarrow A\le36\)
Dấu = xảy ra khi:
12 - 3x = 6 - 2y = 2y + 3x
=> \(\hept{\begin{cases}3x+4y=6\\6x+2y=12\end{cases}\Rightarrow\hept{\begin{cases}x=2\left(n\right)\\y=0\left(n\right)\end{cases}}}\)
Vậy.....
3x² - 6y²+7xy+3x+9y+11=0
Tìm x; y biết x;y là số nguyên
3x2-6y2+7xy +3x +9y +11=0
3x2+ 9xy - 6y2- 2xy +3x +9y =-11
3x(x+ 3y) – 2y(3y+x) +3(x +3y) =-11
(x+ 3y) (3x-2y+3)=-11.1=-1.11
Suy ra x+ 3y = -11 và 3x-2y+3=1 hoặc x+ 3y = -1 và 3x-2y+3=11
Chỉ có trường hợp sau có kết quả x và y nguyên là : x = 2; y = -1
bạn ơi giải cụ thể giúp mình đc k?
giải theo cách lớp 8 thì phải rút x từ phương trình thứ nhất rồi thế vào phương trình thứ 2
x+3y =-11 suy ra x = -11 -3y, thay vào pt thứ 2 ta được:
3.(-11 -3y)-2y + 3=1, tìm được y rồi tìm x
cho x>0 , y>0 , x+y≥ 6 tìm giá trị nhỏ nhất của
P = 3x + 2y + \(\dfrac{6}{x}\) + \(\dfrac{8}{y}\)
\(\Leftrightarrow2P=6x+4y+\dfrac{12}{x}+\dfrac{16}{y}\\ \Leftrightarrow2P=\left(\dfrac{12}{x}+3x\right)+\left(\dfrac{16}{y}+y\right)+3\left(x+y\right)\\ \Leftrightarrow2P\ge2\sqrt{36}+2\sqrt{16}+3\cdot6=12+8+18=38\\ \Leftrightarrow P\ge19\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}3x^2=12\\y^2=16\\x+y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=4\end{matrix}\right.\)
TÌM X. Y NGUYÊN > 0 THỎA MÃN 3x +7 = y( x-3y)
3x+7=y(x-3y)
=>3x-xy+3y^2=7
=>x(3-y)+3y^2-27=-20
=>x(3-y)+3(y-3)(y+3)=-20
=>x(3-y)-3(3-y)(y+3)=-20
=>(3-y)(x-3y-9)=-20
=>(y-3)(x-3y-9)=-20
mà x,y là số nguyên dương
nên (x-3y-9;y-3) thuộc {(-5;4); (-4;5); (-2;10); (-1;20)}
=>(x-3y-9;y) thuộc {(-5;7); (-4;8); (-2;13); (-1;23)}
=>(x,y) thuộc {(29;8); (46;13); (77;23)}
Bài 1 làm tính chia :
a,[5.(x-y)^4-3.(x-y)^3+4.(x-y)^2]:(y-x)^2
b,[(x+y)^5-2.(x+y)^4+3.(x+y)^3]:(3x-1)=0
Bài 2 tìm x biết :
(x^2-1/2x):2x-(3x-1)^2.(3x-1)=0