Cho hình chóp S.ABC có SA=2, SB=3, SC=4. Góc A S B ⏜ = 45 0 , B S C ⏜ = 60 0 . Tính khoảng cách từ điểm B đến mặt phẳng (SAC).
A. 1 2
B. 3
C. 1
D. 3 2
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SA=a; SB=a 2 , SC=a 3 . Tính khoảng cách từ S đến mặt phẳng (ABC).
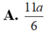
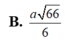
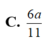
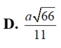
Cho hình chóp S.ABC có các cạnh SA,SB,SC đôi một vuông góc với nhau. Biết SA = 3, SB = 4, SC 5, thể tích khối chóp S.ABC bằng
A. 20.
B. 30.
C. 10.
D. 60.
Phương pháp:
Thể tích tứ diện vuông là V = 1 6 abc
Cách giải:
Thể tích ![]()
Chọn C.
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, S A = S B = S C = a . Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là
A. a 3 3
B. a 3
C. a 3 24
D. a 3 12
Đáp án C
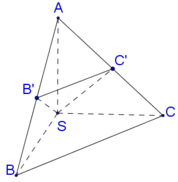
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC.
Ta có:
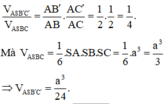
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, SA=SB=SC=a. Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC với SA ⊥ SB , SB ⊥ SC , SC ⊥ SA ; SA = SB = SC = a . Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB, AC. Thể tích của hình chóp S.AB′C′ là
A. a 3 24
B. a 3
C. a 3 3
D. a 3 12
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, SA=SB=SC=a Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là
A. a 3 3
B. a 3
C. a 3 24
D. a 3 12
Chọn C
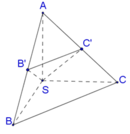
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC
Ta có
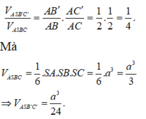
Cho hình chóp S.ABC có SA,SB,SC đôi một vuông góc với nhau và S A = 2 3 ; S B = 2 , S C = 3. Tính thể tích khối chóp S.ABC.
A. V = 6 3
B. V = 4 3
C. V = 2 3
D. V = 12 3
Đáp án C
Thể tích khối chóp S.ABC là
V = 1 6 S A . S B . S C = 1 6 .2 3 .2.3 = 2 3
Cho hình chóp S.ABC có SA;SB;SC đôi một vuông góc với nhau và S A = 2 3 , S B = 2 , S C = 3. Tính thể tích khối chóp S.ABC
A. V = 12 3
B. V = 4 3
C. V = 2 3
D. V = 6 3
Đáp án C
Thể tích khối chóp là V = 1 6 .2 3 .2.3 = 2 3
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và S A = 2 3 , SB=2; SC=3. Tính thể tích khối chóp S.ABC
A. V = 6 3
B. V = 4 3
C. V = 2 3
D. V = 12 3
Cho hình chóp S . A B C có S A = 2 , S B = 3 , S C = 4. Góc A S B ^ = 45 ∘ , B S C ^ = 60 ∘ ,
C S A ^ = 90 ∘ . Tính khoảng cách từ điểm B đến mặt phẳng S A C .
A. 1 2
B. 3
C. 1
D. 3 2
Đáp án D
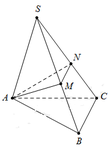
Gọi M, N lần lượt thuộc cạnh SB,SC sao cho S M = S N = 2.
Tam giác SMN đều ⇒ S M = S N = M N = 2.
Tam giác SAM có AS M ^ = 45 ∘ ⇒ A M = 2 2 − 2 .
Tam giác SAN vuông cân tại S ⇒ A N = S A 2 = 2 2 .
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC ⇒ S I ⊥ A M N .
Tính bán kính đường tròn ngoại tiếp Δ A M N . Diện tích tam giác AMN là
S = p p − A M p − A N p − M N ⇒ R Δ A M N = A M . A N . M N 4 S = 2 4 − 2 2 S Δ A M N ,
với p = A M + A N + M N 2 .
Tam giác SAI vuông tại I, có S I = S A 2 − I A 2 = 4 − R 2 Δ A M N .
Ta có V S . A M N V S . A B C = S M S B . S N S C = 2 3 . 2 4 = 1 3 ⇒ V S . A B C = 3 V S . A M N ⇒ d B ; S A C = 9 V S . A M N S Δ S A C = 3 2 .