Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x+2y+z+6=0. Tìm tọa độ điểm M thuộc tia Oz sao cho khoảng cách từ M đến (P) bằng 3.

A .   M ( 0 ; 0 ; 21 )

B .   M ( 0 ; 0 ; 3 )

C .   M ( 0 ; 0 ; 3 ) , M ( 0 ; 0 ; - 15 )

D .   M ( 0 ; 0 ; - 15 )

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x + 2 y + z + 6 = 0 . Tìm tọa độ điểm M thuộc tia Oz sao cho khoảng cách từ M đến (P) bằng 3.

A. M(0;0;21)

B. M(0;0;3)

C. M(0;0;3), M(0;0;-15)

D. M(0;0;-15)

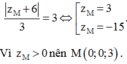
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x+2y+z+6=0.Tìm tọa độ điểm M thuộc tia Oz sao cho khoảng cách từ M đến (P) bằng 3.

A.  M(0;0;3)

B.  M(0;0;3), M(0;0;-15)

C.  M(0;0;-15)

D.  M(0;0;21)

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α):2x-2y-z+3=0 và điểm M(1;-2;13). Tính khoảng cách từ điểm M đến mặt phẳng ( α ) .

A. d(M, ( α ) )= 4/3

B. d(M, ( α ) )= 2/3

C. d(M, ( α ) )= 5/3

D. d(M, ( α ) )= 4

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α :   2 x - 2 y + z - 3 = 0 và điểm M(1;-2;13). Tính khoảng cách từ điểm M đến mặt phẳng (a).

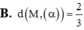
Trong mặt phẳng tọa độ Oxyz, cho mặt phẳng

( α ): x -2y + 2z - 11 = 0 và điểm M (0;1;1). Tính

khoảng cách h từ điểm M đến mặt phẳng ( α ).

A. h = 1

B. h = 2

C. h = 3

D. h = 4

Cho số phức z thỏa mãn iz + 2 - i = 0. Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm  M(3;-4) là:

A. 2 5

B. 13

C. 2 10

D. 2 2

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :   x - 5 2 = y + 7 2 = z - 12 - 1  và mặt phẳng ( α ) :   x+2y-3z-3=0. Gọi M là giao điểm của d với ( α ) , A thuộc d sao cho A M = 14 . Tính khoảng cách từ A đến mặt phẳng  ( α )

A. 2

B. 3.

C. 6.

D. 14

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 5 2 = y + 7 2 = z - 12 - 1  và mặt phẳng α :   x + 2 y   - 3 z - 3 = 0 . Gọi M là giao điểm của d với α , A thuộc d sao cho A M = 14 . Tính khoảng cách từ A đến mặt phẳng α    

A. 2

B. 3.

C. 6

D.  14