Cho một sóng ngang truyền trên mặt nước có phương trình dao động u = 8 cos 2 π ( t o , 1 - 1 2 - x 2 ) mm, trong đó x tính bằng cm, t tính bằng giây. Tốc độ truyền sóng cơ trên mặt nước bằng:
A. 20 cm/s.
B. 30 cm/s.
C. 10 cm/s.
D. 40 cm/s.
Cho một sóng ngang truyền trên mặt nước có phương trình dao động u = 8 cos 2 π t 0 , 1 - 1 2 - x 2 mm, trong đó x tính bằng cm, t tính bằng giây. Tốc độ truyền sóng cơ trên mặt nước bằng:
A. 20 cm/s.
B. 30 cm/s
C. 10 cm/s.
D. 40 cm/s.
Một nguồn sóng O trên mặt nước dao động với phương trình u 0 = 5 c o s ( 2 π t + π/4 ) cm (t đo bằng giây). Tốc độ truyền sóng trên mặt nước 10 cm/s, coi biên độ sóng truyền đi không đổi. Tại các thời điểm t = 1,9s và t = 2,5s điểm M trên mặt nước cách nguồn 20 cm có li độ là bao nhiêu?
A. 2 , 5 2 c m
B. 2,5 cm
C. 3,5 cm
D. 4,5 cm
Hướng dẫn: Chọn đáp án A
Thời gian cần thiết sóng truyền từ O đến M: 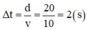
* Khi t = 1,5 s thì sóng chưa truyền đến M nên uM = 0.
* Khi t = 2,5 s thì sóng đã truyền đến rồi, để tìm li độ ta viết phương trình sóng tại M:
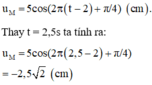
Chú ý: Khi cho biết phương trình sóng u = a cos ω t ∓ 2 π λ x
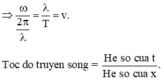
Cho nguồn song O trên mặt nước dao động theo phương trình: u 0 = A cos ω t c m . Điểm M nằm trên một phương truyền sóng cách O là 1/3 bước sóng, ở thời điểm t = T/2 (T là chu kì sóng) thì li độ là 5 cm. Biên độ A bằng:
A. 5,8 cm
B. 7,7 cm
C. 10 cm
D. 8,5 cm
Đáp án C.
Phương trình dao động của điểm M cách O khoảng λ / 2 là:
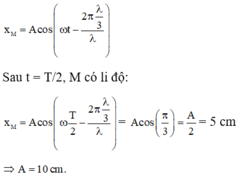
Một nguồn sóng đặt tại điểm O trên mặt nước, dao động theo phương vuông góc với mặt nước với phương trình u = acos40 π t trong đó t tính theo giây. Gọi M và N là hai điểm nằm trên mặt nước sao cho OM vuông góc với ON. Biết tốc độ truyền sóng trên mặt nước bằng 80 cm/s. Khoảng cách từ O đến M và N lần lượt là 34 cm và 50 cm. Số phần tử trên đoạn MN dao động cùng pha với nguồn là
A. 5.
B. 7.
C. 6.
D. 4
Đáp án C
Bước sóng của sóng λ = 2 π v ω = 4cm.
+ Gọi I là một điểm trên MN, phương trình dao động của I có dạng:
u 1 = a 1 cos ω t - π d 1 + d 2 λ .
+ Để I cùng pha với nguồn thì π d 1 + d 2 λ = 2 k π → d 1 + d 2 = 2 k λ = 8k.
Với khoảng giá trị của tổng d 1 + d 2 là O N ≤ d 1 + d 2 ≤ O M + M N .
→ 50 8 ≤ k ≤ 36 + 36 2 + 50 2 8 ↔ 6 , 25 ≤ k ≤ 12 , 2
→ Có 6 điểm dao động cùng pha với nguồn trên MN.
Ở một mặt nước (đủ rộng), tại điểm O có một nguồn sóng dao động theo phương thẳng đứng với phương trình u0 = 4cos20πt (u tính bằng cm, t tính bằng s). Tốc độ truyền sóng trên mặt nước là 40 m/s, coi biên độ sóng không đổi khi sóng truyền đi. Phương trình dao động của phần tử nước tại điểm M (ở mặt nước), cách O một khoảng 50 cm là
A. uM = 4cos(20πt + π 2 ) (cm)
B. uM = 4cos(20πt - π 4 ) (cm)
C. uM = 4cos(20πt - π 2 ) (cm)
D. uM = 4cos(20πt + π 4 ) (cm)
Đáp án: B
HD Giải: λ = vT = ![]() = 4m
= 4m
u = 4cos(20πt - ![]() ) = 4cos(20πt -
) = 4cos(20πt - ![]() )
)
Ở một mặt nước (đủ rộng), tại điểm O có một nguồn sóng dao động theo phương thẳng đứng với phương trình u o = 4 cos 20 πt (u tính bằng cm, t tính bằng s). Tốc độ truyền sóng trên mặt nước là 40 m/s, coi biên độ sóng không đổi khi sóng truyền đi. Phương trình dao động của phần tử nước tại điểm M (ở mặt nước), cách O một khoảng 50 cm là
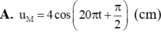
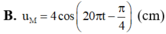
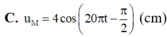
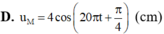
Một nguồn phát sóng cơ dao động theo phương trình u = 4 cos ( 4 πt - π / 4 ) . Biết dao động tại hai điểm gần nhau nhất trên cùng một phương truyền sóng cách nhau 0,5 m có độ lệch pha là 60 0 . Tốc độ truyền của sóng đó là
A. 2,0 m/s.
B. 6,0 m/s.
C. 1,0 m/s
D. 1,5 m/s
Trên mặt nước nằm ngang có hai nguồn sóng S 1 ; S 2 dao động theo phương thẳng đứng với phương trình u 1 = u 2 = 5 cos ( 20 π t + π ) cm và tạo ra hiện tượng giao thoa sóng. Vận tốc truyền sóng trên mặt nước là 20cm/s. Một điểm M trên mặt nước cách S 1 đoạn 16cm và cách S 2 đoạn 20cm. Điểm M thuộc đường
A. cực tiểu thứ 3
B. cực đại bậc 3
C. cực tiểu thứ 2
D. cực đại bậc 2
Trên mặt nước nằm ngang có hai nguồn sóng S 1 , S 2 dao động theo phương thẳng đứng với phương trình u 1 = u 2 = 5 cos ( 20 π t + π ) c m và tạo ra hiện tượng giao thoa sóng. Vận tốc truyền sóng trên mặt nước là 20cm/s. Một điểm M trên mặt nước cách S 1 đoạn 16cm và cách S 2 đoạn 20cm. Điểm M thuộc đường
A. cực tiểu thứ 3
B. cực đại bậc 3
C. cực tiểu thứ 2
D. cực đại bậc 2
Chọn đáp án D
λ = v f = 2 c m ⇒ k = d 2 M − d 1 M λ = 20 − 16 2 = 2 ⇒ Cực đại bậc 2