Cho dãy số xác định bởi u 1 = 2018 u n + 1 = u n 2 + n 2 + 2018 , n ≥ 1 . Số hạng thứ 21 trong dãy số có giá trị gần nhất là
A. 2016
B. 2017
C. 2028
D. 2029
Những câu hỏi liên quan
Cho dãy số xác định bởi
u
1
1
u
n
+
1
2
u
n...
Đọc tiếp
Cho dãy số xác định bởi u 1 = 1 u n + 1 = 2 u n + 5 Tính số hạng thứ 2018 của dãy.
A. u2018 = 3.22018 + 5
B. u2018 = 3.22017 + 1
C. u2018 = 6.22017 – 5
D. u2018 = 6.22018 - 5
Chọn D.
Ta có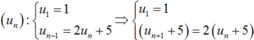 
Đặt: vn = un + 5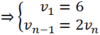 
Khi đó ta được dãy mới; là cấp số nhân với : v1 = 6; q = 2
⇒ v2018 = 22017.v1 = 6.22017 ⇒ u2018 = 6.22017 – 5.
Đúng 0
Bình luận (0)
Cho dãy số
u
n
xác định bởi
u
1
1
u
n
+
1
2...
Đọc tiếp
Cho dãy số u n xác định bởi u 1 = 1 u n + 1 = 2 u n + 5 . Tính số hạng thứ 2018 của dãy.
A. u 2018 = 3.2 2018 + 5
B. u 2018 = 3.2 2017 + 1
C. u 2018 = 6.2 2018 − 5
D. u 2018 = 6.2 2018 − 5
Đáp án D
Ta có: u n : u 1 = 1 u n − 1 = 2 u n + 5 ⇒ u 1 = 1 u n + 1 + 5 = 2 u n + 5
Đặt: v n = u n + 5 ⇒ v 1 = 6 v n − 1 = 2 v n
⇒ v 2018 = 2 2017 . v 1 = 6.2 2017 ⇒ u 2018 = 6.2 2017 − 5
Đúng 0
Bình luận (0)
Cho dãy số
u
n
xác định bởi
u
1
1
u
n
+
1
2...
Đọc tiếp
Cho dãy số u n xác định bởi u 1 = 1 u n + 1 = 2 u n + 5 . Tính số hạng thứ 2018 của dãy.
A. u 2018 = 3.2 2018 + 5
B. u 2018 = 3.2 2017 + 5
C. u 2018 = 3.2 2018 − 5
D. u 2018 = 3.2 2017 − 5
Đáp án C
Phân tích v n + 1 + k = 2 u n + k ⇒ k = 5 ⇒ u n + 1 + 5 = 2 u n + 5
Đặt
v n = u n + 5 ⇒ v n + 1 = 2 v n C S N ⇒ v n = v 1 q n − 1 = u 1 + 5 .2 n − 1 = 6.2 n − 1
⇒ u n + 5 = 6.2 n − 1 ⇒ u 2018 = 6.2 2017 − 5
Đúng 0
Bình luận (0)
Cho dãy số
u
n
xác định bởi
u
1
1
u
n
+
1
2...
Đọc tiếp
Cho dãy số u n xác định bởi u 1 = 1 u n + 1 = 2 u n + 5 Tính số hạng thứ 2018 của dãy số trên
A. u 2018 = 6 . 2 2017 - 5
B. u 2018 = 6 . 2 2018 - 5
C. u 2018 = 6 . 2 2017 + 1
D. u 2018 = 6 . 2 2018 + 5
Cho dãy số xác định bởi u1=1 , u n+1 = \(2un+\frac{n-1}{n^2+3n+2}\). khi đó u 2018 bằng
Cho dãy số (an) xác định bởi
a
n
2017
.
sin
n
π
2
+
2018
.
cos
n
π
3
.Mệnh đề nào dưới đây là mệnh đề đúng? A. an+6 an, ∀ n ∈ R*. B. an+9 an, ∀ n ∈ R*. C. an+12 an, ∀n ∈ R*. D. an+15 an, ∀ n ∈ R*.
Đọc tiếp
Cho dãy số (an) xác định bởi a n = 2017 . sin n π 2 + 2018 . cos n π 3 .Mệnh đề nào dưới đây là mệnh đề đúng?
A. an+6 = an, ∀ n ∈ R*.
B. an+9 = an, ∀ n ∈ R*.
C. an+12 = an, ∀n ∈ R*.
D. an+15 = an, ∀ n ∈ R*.
Chọn C.
Kiểm tra từng phương án đến khi tìm được đáp án đúng.
+ Ta có 
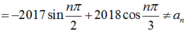
+ Ta có 
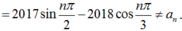
+ Ta có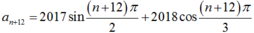 
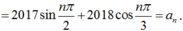
+ Ta có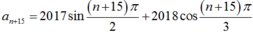 
Đúng 0
Bình luận (0)
cho dãy số un đc xác định bởi công thức \(\left\{{}\begin{matrix}u_1=2018\\u_{n+1}\left(3n^2+9n\right)=\left(n^2+5n+4\right)u_n\end{matrix}\right.\)
Cho dãy số
u
(
n
)
xác định bởi
u
(
1
)
1
;
u
(
m
+
n
)
u...
Đọc tiếp
Cho dãy số u ( n ) xác định bởi u ( 1 ) = 1 ; u ( m + n ) = u ( m ) + u ( n ) + m n , ∀ m , n ∈ ℕ * . Tính u ( 2017 )
A. 2035153
B. 2035154
C. 2035155
D. 2035156
Chọn A
Phương pháp: Tìm công thức số hạng tổng quát
Cách giải: Ta có:
u ( 1 ) = 1
u ( 2 ) = u ( 1 ) + u ( 1 ) = 2 u ( 1 ) + 1
u ( 3 ) = u ( 2 ) + u ( 1 ) = 3 u ( 1 ) + 1 + 2
u ( 4 ) = u ( 3 ) + u ( 1 ) = 4 u ( 1 ) + 1 + 2 + 3
. . .
u ( 2017 ) = u ( 2016 ) + u ( 1 ) = 2017 u ( 1 ) + 1 + 2 + 3 . . . + 2016
⇒ u ( 2017 ) = 1 + 2 + 3 . . . + 2016 + 2017 = 2035153
Đúng 0
Bình luận (0)
Cho dãy số
u
n
được xác định bởi
u
1
2
u
n
+
1...
Đọc tiếp
Cho dãy số u n được xác định bởi u 1 = 2 u n + 1 = 4 u n + 9
Dãy số v n xác định bởi v n = u n + 3 , với mọi n ≥ 1 . Khẳng định nào dưới đây đúng?
A. Dãy v n là cấp số cộng với công sai d=3 .
B. Dãy v n là cấp số nhân với công bội q=4.
C. Dãy v n là cấp số cộng với công sai d=4 .
D. Dãy v n là cấp số nhân với công bội q= 9
