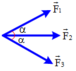
Ba lực đồng quy, đồng phẳng như hình vẽ. Biết độ lớn của các lực F 1 = F 2 = F 3 = 30 3 N ; α = 30 ° . Hợp lực của ba lực trên có độ lớn
A. 125N
B. 154 N
C. 132N
D. 142 N
Hãy dùng quy tắc hình bình hành lực và quy tắc đa giác lực để tìm hợp lực của ba lực F → 1 , F → 2 v à F → 3 có độ lớn bằng nhau và bằng 15N, cùng nằm trong một mặt phẳng. Biết rằng lực F → 2 làm thành với hai lực F → 1 v à F → 3 những góc đều là 60 ° .
Cho 3 lực đồng quy, đồng phẳng F → 1 , F → 2 , F → 3 lần lượt hợp với trục Ox những góc 0 ° , 60 ° , 120 ° ; F 1 = F 3 = 2 F 2 = 30 N . Tìm hợp lực của ba lực trên.
A. 45N
B. 50N
C. 55N
D. 40N
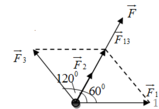
Cho 3 lực đồng quy, đồng phẳng F → 1 , F → 2 , F → 3 lần lượt hợp với trục Ox những góc 0 0 , 60 0 , 120 0 ; F 1 = F 3 = 2 F 2 = 30 N . Tìm hợp lực của ba lực trên.
Theo bài ra ( F 1 → ; F → 3 ) = 120 0 ; F 1 = F 3 nên theo quy tắc tổng hợp hình bình hành và tính chất hình thoi
Ta có ( F 1 → ; F → 13 ) = 60 0 ; F 1 = F 3 = F 13 = 30 N
Mà ( F 1 → ; F → 2 ) = 60 0 ⇒ F → 2 ↑ ↑ F → 13
Vậy F = F 13 + F 2 = 30 + 15 = 45 N
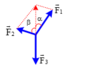
Có 3 lực đồng qui F → 1 ; F → 2 ; F → 3 như sau. Có thể suy ra được (các) kết quả nào bên dưới đây? (F: Độ lớn của lực F → )
A. O
B. F 2 sin α = F 3 sin α + β
C. F h d = G . m 1 m 2 r 2
D. A, B, C đều đúng
Khi tổng hợp hai lực đồng quy F 1 → và F 2 → thành 1 lực F → thì độ lớn của hợp lực F → :
A. luôn nhỏ hơn lực thành phần
B. luôn lớn hơn lực thành phần
C. luôn bằng lực thành phần
D. có thể lớn hơn, nhỏ hơn hoặc bằng lực thành phần
Chọn đáp án D
Độ lớn của lực F nằm trong đoạn
![]()
Cho hai lực đồng quy có cùng độ lớn F 1 = F 2 = F . Góc giữa hai lực bằng bao nhiêu thì hợp lực cũng có độ lớn bằng FN. Vẽ hình minh họa.
Vì F 1 = F nên nếu gọi α là góc hợp bởi hai lực thành phần thì ta có:
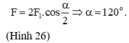
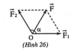
Cho ba lực đồng quy tại O, đồng phẳng ( F 1 → , F 2 → , F 3 → ) lần lượt hợp với trục Ox những góc 0 0 , 60 0 , 120 0 và có độ lớn tương ứng là F 1 = F 3 = 2 F 2 = 10 N như hình vẽ. Tìm hợp lực của ba lực trên?
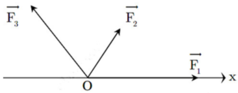
A. 15N
B. 20N
C. 25N
D. 10N
Cách 1:
Lực tổng hợp của ba lực: F → = F 1 → + F 2 → + F 3 →
Tổng hợp hai lực F 1 → , F 2 → ta được F 3 →
( F 1 → ; F 3 → ^ ) = 120 0 F 1 = F 3 = 10 N ⇒ F 13 = F 1 2 + F 3 2 + 2 F 1 F 3 c o s 120 0 = 10 N
Và góc giữa F 13 → với trục Ox là 600 (Δ có ba cạnhF1=F3=F13⇒Δđều)
F → = F 13 → + F 2 →
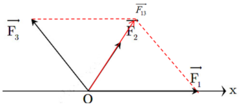
Lại có F 2 → hợp với Ox một góc 600
F 2 → ↑ ↑ F 13 → → F = F 2 + F 13 = 10 + 5 = 15 N
Cách 2:
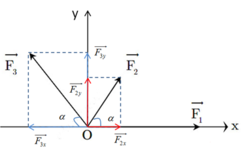
Ta có:F1=F3=2F2=10N
⇒ F 1 = 10 N F 2 = 5 N F 3 = 10 N
(Do đầu bài không có hình nên mình vẽ hướng của các lực như hình dưới nhé)
Phân tích các lực theo các phương Ox và Oy ta được:
F 2 x = F 2 c o s α = 5. c o s 60 0 = 2 , 5 N F 2 y = F 2 s i n α = 5. s i n 60 0 = 2 , 5 3 N
F 3 x = F 3 c o s α = 10. c o s 60 0 = 5 N F 3 y = F 3 s i n α = 10. s i n 60 0 = 5 3 N
Hợp lực theo các phương:
Phương Ox: F x → = F → 1 + F 2 x → + F 3 x →
Chiếu ta được:
F x = F 1 + F 2 x − F 3 x = 10 + 2 , 5 − 5 = 7 , 5 N
Phương Oy: F y → = F 2 y → + F 3 y →
Chiếu ta được:
F y = F 2 y + F 3 y = 2 , 5 3 + 5 3 = 7 , 5 3 N
Lực tổng hợp của 3 lực F 1 → , F 2 → , F 3 → là:
F = F x 2 + F y 2 = 7 , 5 2 + 7 , 5 3 2 = 15 N
Đáp án: A
Khi tổng hợp hai lực đồng quy F 1 v à F 2 thành một lực F thì độ lớn của hợp lực F
A. luôn nhỏ hơn lực thành phần.
B. luôn lớn hơn lực thành phần
C. luôn bằng lực thành phần.
D. có thể lớn hơn, nhỏ hơn hoặc bằng lực thành phần.
Độ lớn F của hợp lực F → của hai lực đồng quy F 1 → v à F 2 → hợp với nhau góc α là:
A. F = F 1 2 + F 2 2 + 2 F 1 F 2 cos α
B. F = F 1 2 + F 2 2 - 2 F 1 F 2 cos α
C. F = F 1 2 + F 2 2 + F 1 F 2 cos α
D. F = F 1 2 + F 2 2 + 2 F 1 F 2