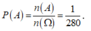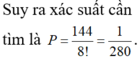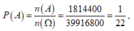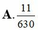Xếp ngẫu nhiên 10 học sinh gồm 5 học sinh nam và 5 học sinh nữ thành một hàng ngang. Xác suất để trong 10 học sinh trên không có hai học sinh cùng giới tính đứng cạnh nhau, đồng thời Hoàng và Lan không đứng cạnh nhau bằng
A. 1 450 .
B. 8 1575 .
C. 1 175 .
D. 4 1575 .