Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, A C = 2 a 3 3 , B A C ⏜ = 60 0 , SA vuông góc với mặt phẳng đáy, SA=a 3 . Khoảng cách giữa hai đường thẳng AC và SB
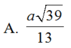
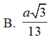
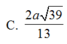
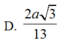
: Cho hình chóp sabcd có đáy ABCD là hình chữ nhật, ab=a, bc=a căn 3, sa vuông góc với (abcd) Góc giữa SC và mặt đáy bằng 45. Khoảng cách từ điểm A đến mặt phẳng (scd) bằng
Hình chóp SABCD có đáy ABCD là hình chữ nhật có AD = 2a. SA = SB = a;
(SAD) ⊥ (ABCD). Tính thể tích V của hình chóp.
A. V = a 3 6 6
B. V = a 3 3 6
C. V = 2 a 3 3
D. V = a 3 3 3
Cho hình chóp SABCD đáy ABCD là hình chữ nhật tâm I ,AB =a, BC=a căn 3 .Tam giác SIA cân tại S . (SAD) vuông góc với đáy .góc giữa SD và (ABCD) = 60* .Tính thể tích khối chóp SABCI?
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật. AB=2a, AD= a√3 , SA vuông góc với đáy (ABCD). Gọi M là trung điểm CD. Góc giữa SM và đáy (ABCD) là 60 độ. Tính khoảng cách giữa hai đường thẳng AM và SB.
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SMA}\) là góc giữa SM và đáy
\(\Rightarrow\widehat{SMA}=60^0\Rightarrow SA=AM.tan60^0=\sqrt{3a^2+\left(\dfrac{2a}{2}\right)^2}.\sqrt{3}=2a\sqrt{3}\)
Qua B kẻ đường thẳng song song AM cắt AD kéo dài tại E
\(\Rightarrow AM||\left(SBE\right)\Rightarrow d\left(AM;SB\right)=d\left(AM;\left(SBE\right)\right)=d\left(A;\left(SBE\right)\right)\)
Từ A kẻ \(AH\perp BE\) , từ A kẻ \(AK\perp SH\Rightarrow AK=d\left(A;\left(SBE\right)\right)\)
\(\widehat{DAM}=\widehat{AEB}\) (đồng vị) , mà \(\widehat{BAH}=\widehat{AEB}\) (cùng phụ \(\widehat{ABH}\))
\(\Rightarrow\widehat{DAM}=\widehat{BAH}\)
\(\Rightarrow AH=AB.cos\widehat{BAH}=AB.cos\widehat{DAM}=\dfrac{AB.AD}{AM}=\dfrac{2a.a\sqrt{3}}{2a}=a\sqrt{3}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}=\dfrac{1}{3a^2}+\dfrac{1}{12a^2}=\dfrac{5}{12a^2}\)
\(\Rightarrow AK=\dfrac{2a\sqrt{15}}{5}\)
Cho hình chóp SABCD có đáy là hình chữ nhật, AB=2a, BC=a. Hình chiếu vuông góc của S trên (ABCD) là trung điểm H của AD, S H = a 3 2 . Tính diện tích mặt cầu ngoại tiếp hình chóp SABCD
A. 4 πa 2 3
B. 16 πa 2 3
C. 16 πa 2 3
D. 4 πa 3 3
Cho hình chóp SABCD có đáy (ABCD) là hình chữ nhật AB=a, AD=a\(\sqrt{3}\). Cạnh bên SA vuông góc với mặt phẳng (ABCD) và SA=a. Góc giữa đường thẳng SB và CD bằng?help pls
Hình chóp SABCD có đáy ABCD là hình chữ nhật. S A ⊥ A B C D Biết S A = a , B C = a 3 , C D = 2 a . Tính bán kính R của mặt cầu ngoại tiếp SABCD
![]()
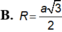
![]()
![]()
Cho hình chóp SABCD, SA vuông góc (ABCD) , ABCD là hình chữ nhật có AB = a , AD 2a , góc hợp bởi (SBC) và đáy là 60° . Tính chiều cao và thể tích khối chóp
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, AB=a. Cạnh bên SA vuông góc với đáy và SA=a. Góc giữa đường thẳng SB và CD là:
A. 90 o
B. 60 o
C. 30 o
D. 45 o
Chọn D.
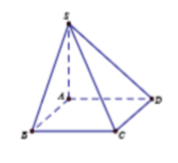
Ta có AB//CD
⇒ S B ; C D ^ = S B ; A B ^ = S B A ^ = 45 o d o ∆ S B A c â n