Cho hai số thực dương x,y thỏa mãn ![]() . Giá trị lớn nhất của biểu thức
. Giá trị lớn nhất của biểu thức ![]() là:
là:
A. 18
B. 12
C. 16
D. 21
Cho x; y là các số thực dương thỏa mãn xy = 4; x ≥ 1 2 ; y ≥ 1 . Tìm giá trị lớn nhất của biểu thức
P = log 1 2 x 3 + log 1 2 y - 1 3
A. - 27 4
B. 0
C. - 4 27
D. -9
Thay y = 4 x vào biểu thức P và biến đổi ta thu được
P = - 9 log 2 2 + 27 log 2 x - 27 .
Do y ≥ 1 nên x ≤ 4 . Suy ra 1 2 ≤ x ≤ 4 . Đặt t = log 2 x , khi đó - 1 ≤ t ≤ 2 .
Xét hàm số f(t0 = - 9 t 2 + 27t - 27; t ∈ - 1 ; 2
Ta có f ' (t) = -18t + 27; f ' (t) = 0 ⇔ t = 3 2
f (-1) = -63; f (2) = -9; f 3 2 = 27 4
Vậy
m a x P = - 27 4 ⇔ x = 2 2 ; y = 2
Đáp án A
Cho $x$, $y$ là các số thực dương thỏa mãn $x + y \le 3$. Tìm giá trị nhỏ nhất của biểu thức $Q = x^2 + y^2 - 9 x - 12 y + \dfrac{16}{2x+y} + 25.$
Cho x, y là các số thực dương thỏa mãn điều kiện 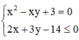 Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức ![]()
A. 12
B. 8
C. 0
D. 4
Đáp án C
Phương pháp:
Rút y theo x từ phương trình (1), thế vào phương trình (2) để tìm khoảng giá trị của x.
Đưa biểu thức P về 1 ẩn x và tìm GTLN, GTNN của biểu thức P.
Cách giải: 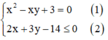
Ta nhận thấy x = 0 không thỏa mãn phương trình (1), do đó 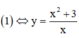 thế vào (2):
thế vào (2):
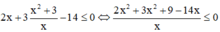
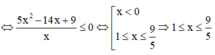
![]()
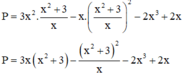
Sử dụng MTCT ta tính được
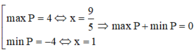
Cho hai số thực dương a, b thỏa mãn 9 a 3 + a b + 1 = 3 b + 2 . Giá trị lớn nhất của biểu thức S = 6a - b là
A. 17 12
B. 82 3
C. 11 3
D. 89 12
Đáp án C
Ta có: 9 a 3 + a b + 1 = 3 b + 2 ⇔ 9 a 3 + a = b + 1 3 b + 2
Đặt t = 3 b + 2 ⇒ b = t 2 - 2 3 ⇒ 9 a 3 + a = t 2 + 1 3 t ⇔ 27 a 3 + 3 a = t 3 + t ⇔ 3 a 3 + 3 a = t 3 + t
Xét hàm số f u = u 3 + u u ∈ ℝ ⇒ f ' u = 3 u 2 + 1 > 0 ∀ u ∈ ℝ ⇒ f u đồng biến trên ℝ
Khi đó: f 3 a = f t ⇔ t = 3 a ⇒ 3 b + 2 = 3 a ⇔ b = 9 a 2 - 2 3
Suy ra S = 6 a - 3 a 2 + 2 3 = - 3 a - 1 2 + 11 3 ≤ 11 3 .
Do đó giá trị lớn nhất của biểu thức S = 6a - b là 11 3 .
Cho hai số thực dương x,y thỏa mãn 2x + 2y = 4. Tìm giá trị lớn nhất Pmax của biểu thức
P = (2x2 + y)(2y2 + x) + 9xy.
A. Pmax = 27 2
B. Pmax = 18
C. Pmax = 27
D. Pmax = 12
Đáp án B.
Ta có 4 = 2 x + 2 y ≥ 2 2 x . 2 y = 2 2 x + y
⇔ 4 ≥ 2 x + y ⇔ x + y ≤ 2 .
Suy ra x y ≤ x + y 2 2 = 1
Khi đó
P = 2 x 3 + y 3 + 4 x 2 y 2 + 10 x y 2 x + y x + y 2 - 3 x y + 2 x y 2 + 10 x y
≤ 4 4 - 3 x y + 4 x 2 y 2 + 10 x y
= 16 + 2 x 2 y 2 + 2 x y x y - 1 ≤ 18
Vậy Pmax = 18 khi x = y = 1.
Cho hai số thực dương x,y thỏa mãn 2 x + 2 y = 4 . Tìm giá trị lớn nhất P m a x của biểu thức P = 2 x 2 + y 2 y 2 + x + 9 x y .
A. 26
B. 18
C. 27
D. 12
Cho hai số thực dương x,y thỏa mãn 2 x + 2 y = 4 . Tìm giá trị lớn nhất P m a x của biểu thức P = 2 x 2 + y 2 y 2 + x + 9 x y
A. P m a x = 27 2
B. P m a x = 18
C. P m a x = 27
D. P m a x = 12
cho x,y là hai số thực dương thỏa mãn x+y≤xy.Tìm giá trị lớn nhất của biểu thức M=\(\dfrac{1}{2x^2+3y^2}+\dfrac{1}{3x^2+2y^2}\)
\(x+y\le xy\Rightarrow\dfrac{1}{x}+\dfrac{1}{y}\le1\)
\(M=\dfrac{1}{2\left(x^2+y^2\right)+y^2}+\dfrac{1}{2\left(x^2+y^2\right)+x^2}\le\dfrac{1}{4xy+y^2}+\dfrac{1}{4xy+x^2}\)
\(B\le\dfrac{1}{25}\left(\dfrac{4}{xy}+\dfrac{1}{y^2}\right)+\dfrac{1}{25}\left(\dfrac{4}{xy}+\dfrac{1}{x^2}\right)=\dfrac{1}{25}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{2}{xy}+\dfrac{6}{xy}\right)\)
\(M\le\dfrac{1}{25}\left[\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2+\dfrac{3}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\right]=\dfrac{1}{10}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\le\dfrac{1}{10}\)
\(M_{max}=\dfrac{1}{10}\) khi \(x=y=2\)
Cho x và y là hai số thực dương thỏa mãn 3x+y ≤4
Tìm giá trị nhỏ nhất của biểu thức A=1/x + 1/√(xy)
Lời giải:
Áp dụng BĐT Cô-si và Cauchy-Schwarz cho các số dương ta có:
$A=\frac{1}{x}+\frac{1}{\sqrt{xy}}\geq \frac{1}{x}+\frac{1}{\frac{x+y}{2}}=\frac{1}{x}+\frac{2}{x+y}=2(\frac{1}{2x}+\frac{1}{x+y})$
$\geq 2.\frac{4}{2x+x+y}=\frac{8}{3x+y}\geq \frac{8}{4}=2$
Vậy $A_{\min}=2$. Giá trị này đạt được tại $x=y; 3x+y=4\Leftrightarrow x=y=1$