Tìm thể tích của hình chóp S.ABC biết S A = a , S B = a 2 , S C = 2 a và có B S A ^ = 60 ° , B S C ^ = 90 ° , C S A ^ = 120 °
A. a 3 6 12
B. a 3 2 3
C. a 3 3 6
D. a 3 3
Những câu hỏi liên quan
Tìm thể tích của hình chóp S.ABC biết SA a, SB
a
2
, SC 2a và có
B
S
A
^
60
∘
,
C
S
A
^
60
∘...
Đọc tiếp
Tìm thể tích của hình chóp S.ABC biết SA = a, SB = a 2 , SC = 2a và có B S A ^ = 60 ∘ , C S A ^ = 60 ∘ , B S C ^ = 60 ∘
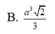
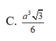
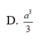
Cho hình chóp S.ABC có SA vuông góc với mp (SBC), SB vuông góc SC; biết SA=3cm, SB=4cm, SC=5cm
a)tính thể tích khối chóp S.ABC
b)Tính khoảng cách từ điểm S đến mp (ABC)
Xét các hình chóp S.ABC thỏa mãn SAa;SB2a;SC3a với a là hằng số cho trước. Tìm giá trị lớn nhất của thể tích khối chóp S.ABC? A. 6
a
3
B. 2
a
3
C.
a
3
D. 3
a
3
Đọc tiếp
Xét các hình chóp S.ABC thỏa mãn SA=a;SB=2a;SC=3a với a là hằng số cho trước. Tìm giá trị lớn nhất của thể tích khối chóp S.ABC?
A. 6 a 3
B. 2 a 3
C. a 3
D. 3 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a (a 0). Hai mặt phẳng (SBC) và (SCD) cùng tạo với mặt phẳng (ABCD) một góc
45
∘
. Biết SB a và hình chiếu của S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính thể tích khối chóp S.ABCD
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a (a > 0). Hai mặt phẳng (SBC) và (SCD) cùng tạo với mặt phẳng (ABCD) một góc 45 ∘ . Biết SB = a và hình chiếu của S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính thể tích khối chóp S.ABCD
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a
a
0
. Hai mặt phẳng (SBC) và
S
C
D
cùng tạo với mặt phẳng (ABCD) một góc
45
°
. Biết
S
B
a
và hình chiếu của S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính thể tí...
Đọc tiếp
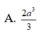
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a a > 0 . Hai mặt phẳng (SBC) và S C D cùng tạo với mặt phẳng (ABCD) một góc 45 ° . Biết S B = a và hình chiếu của S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính thể tích khối chóp S.ABCD
A. 2 a 3 3
B. 2 a 3 6
C. a 3 4
D. 2 a 3 9
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Biết khoảng cách giữa hai đường thẳng BC và SM bằng
a
3
4
. Tính thể tích của khối chóp đã cho theo a. A.
a
3
3
4...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Biết khoảng cách giữa hai đường thẳng BC và SM bằng a 3 4 . Tính thể tích của khối chóp đã cho theo a.
A. a 3 3 4
B. a 3 3 2
C. a 3 3 6
D. a 3 3 12
Chọn C
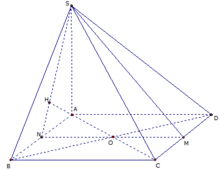
Gọi N là trung điểm của AB => BC // (SMN)
Suy ra d (BC, SM)=d (BC, (SMN))=d (B, (SMN))=d (A, (SMN)).
Dựng AH vuông góc với SN tại H
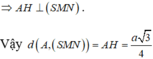
Lại có, trong tam giác vuông SAN:
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD) và ABCD là hình vuông cạnh a, góc giữa SC và mặt phẳng (ABCD) bằng
45
∘
. Mặt phẳng (
α
) qua A và vuông góc với SC và chia khối chóp S.ABCD thành hai khối đa diện. Gọi
V
1
là thể tích của khối đa diện có chứa điểm S và
V
2
là thể tích của khối đa...
Đọc tiếp
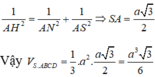
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD) và ABCD là hình vuông cạnh a, góc giữa SC và mặt phẳng (ABCD) bằng 45 ∘ . Mặt phẳng ( α ) qua A và vuông góc với SC và chia khối chóp S.ABCD thành hai khối đa diện. Gọi V 1 là thể tích của khối đa diện có chứa điểm S và V 2 là thể tích của khối đa diện còn lại. Tìm tỉ số V 1 V 2 ?
A. 1
A. 1 3
C. 1 2
D. 4 5
Cho hình chóp tứ giác đều S.ABCD, đấy là hình vuông cạnh bằng 10cm, biết SA=13cm. Tính diện tích xung quanh và diện tích toàn phần và thể tích của hình chóp trên.
Ta có:
AI=\(\dfrac{AB}{2}=5cm\)
Áp dụng định lý Pitago vào △SIA
⇒ SI2+AI2=SA2 ⇒ SI=√(SA2-AI2)=12 cm
nên Sxq ABCD=p.d=\(\dfrac{1}{2}\).10.4.12=240 cm2
Áp dụng định lý Pitago vào △ABC
⇒ AC2=AB2+BC2 ⇒ AC=√(102+102)=10√2 cm
Ta có: OA=\(\dfrac{AC}{2}\)=5√2 cm
Áp dụng định lý Pitago vào △SOA
⇒ SA2=SO2+SA2 ⇒ SO=√[132-(5√2)2]=√119 cm
nên VABCD=\(\dfrac{1}{3}\).10.4.√119≈145,45 cm3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABCD là tam giác vuông tại C, AB
5
a,ACa. Cạnh SA3a và vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng A.
a
3
B.
5
2
a
3
C.
2
a
3
D.
3
a
3
Đọc tiếp
Cho hình chóp S.ABC có đáy ABCD là tam giác vuông tại C, AB= 5 a,AC=a. Cạnh SA=3a và vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng
A. a 3
B. 5 2 a 3
C. 2 a 3
D. 3 a 3
