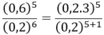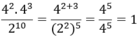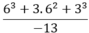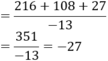Tính giá trị của biếu thức sau: 2 7 . 9 3 6 5 . 8 2

Những câu hỏi liên quan
Tính giá trị của biếu thức sau: 0 , 6 5 0 , 2 6
Tính giá trị của biếu thức sau: 4 2 . 4 3 2 10
Tính giá trị của biếu thức sau: 6 3 + 3 . 6 2 + 3 3 - 13
Tìm giá trị nhỏ nhất của các biếu thức sau:
3) A= | x-3| -7
4) A= | x-5| + 2015
3) |x -3| > 0 => A = |x - 3| - 7 > -7
=> GTNN của A là -7 <=> |x - 3| = 0 <=> x = 3
4) |x - 5| > 0 => A = |x - 5| + 2015 > 2015
=> GTNN của A là 2015 <=> |x - 5| = 0 <=> x = 5
Đúng 0
Bình luận (0)
3). A=|x-3|-7
Vì |x-3| > 0 => |x-3|-7 > -7
Vậy MinA = -7 => |x-3| =0
=> x=3
4). A=|x-5|+2015
Vì |x-5| > 0 => |x-5|+2015 > 2015
Vậy MinA = 2015 => |x-5| =0
=> x=5
Đúng 0
Bình luận (0)
tính giá trị biếu thức A 3 mũ 10 . 11 3 mũ 10 . 5 trên 3 mũ 9 . 2 mũ 4giúp mình với mình cần gấp dấu chấm là nhân nha
Xem chi tiết
cho biếu thức: \(A=\left(\frac{x}{x+1}+\frac{2}{x-3}+\frac{x^{2+3}}{9-x^2}\right):\frac{-2}{x+2}\)
a) Tìm điều kiện xác định của biểu thức A
b) Rút gọn biểu thức A
c) Tính giá trị của biểu thức A khi x=3
d) Tìm các giá trị nguyên của x để A có giá trị nguyên
câu a, phân tích từng mẫu thành nhân tử (nếu cần)
rồi tìm mtc, ở đây, nhân chia cũng như cộng trừ, nên phân tích hết rồi ra mtc, đkxđ là cái mtc ấy khác 0
câu b với c tự làm
câu d thì lấy cái rút gọn rồi của câu b, rồi giải ra, để nguyên thì mẫu là ước của tử, thế thôi
Đúng 0
Bình luận (3)
1. Tìm các giá trị nguyên của x để các biểu thức sau có giá trị lớn nhấta. A1/7-x b.B27-2x/12-X2.Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nhỏ nhấta. A1/x-3 b. B 7-x/x-5 c. C 5x-19/x-43.Tìm giá trị nhỏ nhất của các biếu thức saua. Ax^4+3x^2 +2 b. B(x^4+5)^2 c. C(x-1)^2+(y+2)^24.Tìm giá trị lớn nhất của các biểu thức saua. A5-3(2x-1)^2 b.B1/2(x-1)^2+3 c. Cx^2+8/x^2+2
Đọc tiếp
1. Tìm các giá trị nguyên của x để các biểu thức sau có giá trị lớn nhất
a. A=1/7-x b.B=27-2x/12-X
2.Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nhỏ nhất
a. A=1/x-3 b. B= 7-x/x-5 c. C= 5x-19/x-4
3.Tìm giá trị nhỏ nhất của các biếu thức sau
a. A=x^4+3x^2 +2 b. B=(x^4+5)^2 c. C=(x-1)^2+(y+2)^2
4.Tìm giá trị lớn nhất của các biểu thức sau
a. A=5-3(2x-1)^2 b.B=1/2(x-1)^2+3 c. C=x^2+8/x^2+2
Tính giá trị biếu thức
a) 23.15 -[115-(12-5)2 ]
b)5.[(85 - 35 : 7) :8 + 90 ] - 50
c){[261 - ( 36-31)3.2 ]-9}.1001
d)3.102 - [1200 - ( 42 - 2.3)3]
\(a)2^3\cdot15-[115-(12-5)^2]\\=8\cdot15-(115-7^2)\\=120-(115-49)\\=120-66\\=54\\---\\b)5\cdot[(85-35:7):8+90]-60\\=5\cdot[(85-5):8+90]-60\\=5\cdot(80:8+90)-60\\=5\cdot(10+90)-60\\=5\cdot100-60\\=500-60\\=440\)
\(---\)
\(c,\left\{\left[261-\left(36-31\right)^3\cdot2\right]-9\right\}\cdot1001\)
\(=\left[\left(261-5^3\cdot2\right)-9\right]\cdot1001\)
\(=\left[\left(261-125\cdot2\right)-9\right]\cdot1001\)
\(=\left[\left(261-250\right)-9\right]\cdot1001\)
\(=\left(11-9\right)\cdot1001\)
\(=2\cdot1001\)
\(=2002\)
\(---\)
\(d,3\cdot10^2-\left[1200-\left(4^2-2\cdot3\right)^3\right]\)
\(=3\cdot100-\left[1200-\left(16-6\right)^3\right]\)
\(=300-\left(1200-10^3\right)\)
\(=300-\left(1200-1000\right)\)
\(=300-200\)
\(=100\)
#\(Toru\)
Đúng 1
Bình luận (0)
a) 23.15 -[115-(12-5)2 ]
= 23.15 -[115-36]
= 8.15 -79
= 120-79
=41
b)5.[(85 - 35 : 7) :8 + 90 ] - 50
=5 .[80:8+90]-50
=5.100-50
=500-50
=450
c){[261 - ( 36-31)3.2 ]-9}.1001
={[261 - 125.2 ]-9}.1001
={[261 -250 ]-9}.1001
={11-9}.1001
=2.1001
=2002
d)3.102 - [1200 - ( 42 - 2.3)3]
=3.100-[1200 -(16-6)3 ]
=300-[1200-1000]
=300-200
=100
Đúng 1
Bình luận (2)
3x2+4x-7=0 A/ chứng tỏ phương trình có 2 nghiệm phân biệt B/ không giải phương trình, hay tính giá trị của biếu thức 2x1-(x1-x2-x1x2(
a) Do a = 3; c = -7 nên a và c trái dấu
Vậy phương trình luôn có hai nghiệm phân biệt
b) Theo Viét ta có:
x₁ + x₂ = -4/3
x₁x₂ = -7/3
Ta có:
2x₁ - (x₁ - x₂ - x₁x₂)
= 2x₁ - x₁ + x₂ + x₁x₂
= x₁ + x₂ + x₁x₂
= -4/3 - 7/3
= -11/3
Đúng 1
Bình luận (1)
\(3x^2+4x-7=0\)
\(a,\) Để pt có 2 nghiệm phân biệt thì \(\Delta>0\Rightarrow4^2-4.3.\left(-7\right)=100>0\)
Vậy pt có 2 nghiệm phân biệt \(x_1,x_2\)
\(b,\)Theo Vi-ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{4}{3}\\x_1x_2=\dfrac{c}{a}=-\dfrac{7}{3}\end{matrix}\right.\)
Ta có : \(2x_1-\left(x_1-x_2-x_1x_2\right)\)
\(=2x_1-x_1+x_2-x_1x_2\)
\(=x_1+x_2-x_1x_2\)
\(=-\dfrac{4}{3}-\left(-\dfrac{7}{3}\right)\)
\(=-\dfrac{4}{3}+\dfrac{7}{3}\)
\(=\dfrac{3}{3}=1\)
Vậy giá trị của biểu thức là \(1\)
Đúng 0
Bình luận (1)