Tổng các nghiệm của phương trình cos4x+12 sin 2 x -1 = 0 trong khoảng - π ; 3 π là:
A. x = k π
B. x = 2 π
C. x = 3 π
D. x = 3 π 2
Tổng các nghiệm của phương trình cos4x+ 12 sin 2 x - 1 = 0 trong khoảng - π ; 3 π là:
A. x = k π
B. x = 2 π
C. x = 3 π
D. x = 3 π 2
Tổng các nghiệm của phương trình c o s 4 x + 12 sin 2 x - 1 = 0 trong khoảng ( - π ; 3 π ) là
A. x = k π
B. x = 2 π
C. x = 3 π
D. x = 3 π 2
Trong các khoảng sau, m thuộc khoảng nào để phương trình sin^2 x-(2m+1) sin x.cos x + 2m cos^2 x = 0 có nghiệm thuộc khoảng (π/4 ; π/3)?
\(sin^2x-2m.sinx.cosx-sinx.cosx+2mcos^2x=0\)
\(\Leftrightarrow sinx\left(sinx-cosx\right)-2mcosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2m.cosx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=2m.cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=2m\end{matrix}\right.\)
Do \(tanx=1\) ko có nghiệm đã cho nên \(tanx=2m\) phải có nghiệm trên khoảng đã cho
\(\Rightarrow tan\left(\dfrac{\pi}{4}\right)< 2m< tan\left(\dfrac{\pi}{3}\right)\)
\(\Rightarrow1< 2m< \sqrt[]{3}\)
\(\Rightarrow m\in\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\) (hoặc có thể 1 đáp án là tập con của tập này cũng được)
Tính tổng tất cả các nghiệm của phương trình cos 5 x cos x = cos 4 x cos 2 x + 3 cos 2 x + 1 thuộc khoảng - π ; π
![]()
![]()
![]()
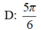
Phương trình sin ( 2 x - π 4 ) = sin ( x + 3 π 4 ) có tổng các nghiệm thuộc khoảng 0 , π bằng:
![]()
![]()
![]()
![]()
Tính tổng S các nghiệm của phương trình (2 cos2 x+5) ( s i n 4 x - c o s 4 x ) +3=0 trong khoảng ( 0 ; 2 π )
A. S=11 π /6
B. S=4 π
C. S=5 π
D. S=7 π /6
Tìm số nghiệm của phương trình sin 2 x + sin x - 1 2 sin x - 1 sin 2 x = 2 c o t 2 x trong khoảng 0 ; π
A. 2
B. 3
C.4
D. 5
Tính tổng các nghiệm trong khoảng − π ; π của phương trình cos x − 1 = 0 .
A. ‒2
B. 0
C. 2
D. 2 arccos 2 3
Tính tổng các nghiệm trong khoảng - π , π của phương trình cos x - 1 = 0 .
A. -2
B. 0
C. 2
D. 2 a r c cos 2 3