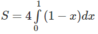Tính diện tích hình phẳng giới hạn bởi các đường sau: y = 2x – x 2 , x + y = 2

Những câu hỏi liên quan
Tính diện tích hình phẳng giới hạn bởi các đường sau: y xsin2x, y 2x,
x
π
2
A.
π
2
4
-
4
B.
π
2
-
π
C.
π
2
4
-
π...
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi các đường sau: y = xsin2x, y = 2x, x = π 2
A. π 2 4 - 4
B. π 2 - π
C. π 2 4 - π 4
D. π 2 4 + π 4
/
Chọn C.
Phương trình hoành độ giao điểm: x sin 2x = 2x <=> x (sin2x-2) = 0 <=> x = 0 hoặc sin2x = 2 (VN)
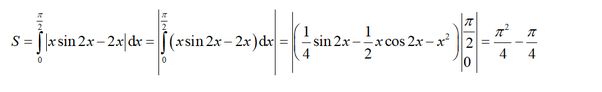
Đúng 0
Bình luận (0)
Tính diện tích hình phẳng giới hạn bởi các đường
y
x
3
−
2
x
;
y
x
−
2
về phía bên trái trục tung. A.
3
4
B.
4
π
3
C. 6 D.
27
4
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi các đường y = x 3 − 2 x ; y = x − 2 về phía bên trái trục tung.
A. 3 4
B. 4 π 3
C. 6
D. 27 4
Tính diện tích miền hình phẳng giới hạn bởi các đường
y
x
2
-
2
x
,
y
0
,
x
-
10
,
x
10
A. S2000/3 B. S2008 C. S2008/3 D. 2000
Đọc tiếp
Tính diện tích miền hình phẳng giới hạn bởi các đường y = x 2 - 2 x , y = 0 , x = - 10 , x = 10
A. S=2000/3
B. S=2008
C. S=2008/3
D. 2000
Diện tích hình phẳng được giới hạn bởi các đường
y
2
x
-
x
2
và đường thẳng
x
+
y
2
là: A.
1
6
d
v
t
t
B.
5
2...
Đọc tiếp
Diện tích hình phẳng được giới hạn bởi các đường y = 2 x - x 2 và đường thẳng x + y = 2 là:
A. 1 6 d v t t
B. 5 2 d v t t
C. 6 5 d v t t
D. 1 2 d v t t
Chọn A.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = 2x - x2 và x + y = 2 là :
![]()
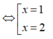
![]()
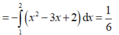
Đúng 0
Bình luận (0)
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số
y
2
x
-
1
2
, trục hoành và các đường thẳng x 2 và x 8. A.
12
7
B.
9
C.
12
D.
10
Đọc tiếp
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = 2 x - 1 2 , trục hoành và các đường thẳng x = 2 và x = 8.
A. 12 7
B. 9
C. 12
D. 10
Cho hình phẳng giới hạn bởi đồ thị các hàm số
y
x
, đường thẳng y 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là A.
7
6
.
B.
4
3
.
C.
5
6
.
D.
5
4
.
Đọc tiếp
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
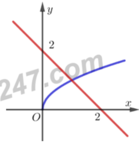
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Biết diện tích hình phẳng giới hạn bởi đường cong yf(x), y0, x2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong yf(2x), trục hoành Ox và hai đường thẳng x0, xa bằng:
Đọc tiếp
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
![]()
![]()
Tính diện tích hình phẳng giới hạn bởi các đường sau: x + y = 1, x + y = -1, x – y = 1, x – y = -1
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.