Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = sin x , trục hoành và hai đường thẳng x = π ; x = 3 π 2 là
A.1
B. 1/2
C. 2
D.3/2
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = x , trục hoành và hai đường thẳng x=1 ; x=4 là
A.4
B.14/5
C.13/3
D.14/3
Ta có x ≥ 0 trên đoạn [1;4] nên
 \
\
Chọn D
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y= e 2 x , trục hoành và hai đường thẳng x=0 ; x=3 là
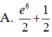
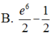


Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y= x 3 , trục hoành và hai đường thẳng x= 1; x=3 là
A.19
B.18
C.20
D.21
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y= x 3 , trục hoành và hai đường thẳng x=1 ; x=8 là
A.45/2
B.45/4
C.45/7
D.45/8
Ta có x 3 ≥ 0 trên đoạn [1 ; 8] nên
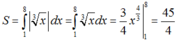
Chọn B
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y= tanx , trục hoành và hai đường thẳng x = π 6 ; x = π 4 , là
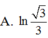
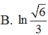
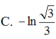
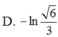
Diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y = x 2 , trục hoành và hai đường thẳng x = - 1 , x = 3 l à :
A. 28 9 d v t t
B. 28 3 d v t t
C. 1 3 d v t t
D. Tất cả đều sai
Chọn B.
Phương trình hoành độ giao điểm của đồ thị hàm số y = x2 và trục hoành: x2 = 0 ⇔ x = 0.
Mà hàm số y = x2 không đổi dấu trên [-1;3] nên:

Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
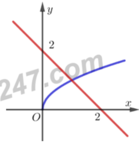
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Tính diện tích hình phẳng giới hạn bởi: Đồ thị hàm số y = x 3 , trục hoành và hai đường thẳng x = -2, x = 2
A.6
B. 7
C. 8
D.9
Ta có trên [-2;0] , x 3 ≤ 0 . Trên [0; 2], x 3 ≥ 0
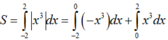
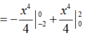
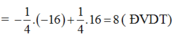
Chọn C
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 1 x , trục hoành và hai đường thẳng x = 1 và x = 2 e là
A. S = ln 2 .
B. 𝑆 = 2 ln 2 .
C. S = ln 2 + 1 .
D. S = 2 ln 2 + 1 .
Đáp án C
Diện tích hình phẳng cần tính là
S = ∫ 1 2 e 1 x d x = ∫ 1 2 e 1 x d x = ln x 1 2 e = ln 2 e = ln 2 + 1 .