Chọn B.
Phương trình hoành độ giao điểm của đồ thị hàm số y = x2 và trục hoành: x2 = 0 ⇔ x = 0.
Mà hàm số y = x2 không đổi dấu trên [-1;3] nên:

Chọn B.
Phương trình hoành độ giao điểm của đồ thị hàm số y = x2 và trục hoành: x2 = 0 ⇔ x = 0.
Mà hàm số y = x2 không đổi dấu trên [-1;3] nên:

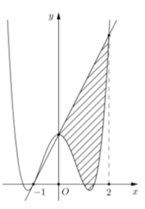
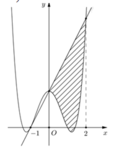
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x = 0 có diện tích bằng:
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Cho hàm số y = f(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x=a; x=b. Diện tích hình phẳng D được tính bởi công thức.
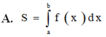
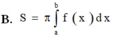
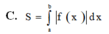
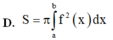
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của A cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ).Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x = 0; x=2 có diện tích bằng
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y= x 3 , trục hoành và hai đường thẳng x= 1; x=3 là
A.19
B.18
C.20
D.21
Cho hàm số y =f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số y = f)x), trục hoành và hai đường thẳng x=a; x=b (a<b). Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức
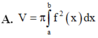
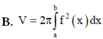
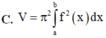

Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y= e 2 x , trục hoành và hai đường thẳng x=0 ; x=3 là
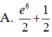
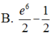


Cho hàm số y = f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x=a; x=b. Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức
![]()
![]()
![]()
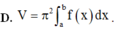
Cho hàm số y = f(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x =a; x=n Thể tích của khối của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:

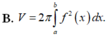
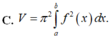
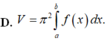
Cho hàm số y=f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y= -9 tại điểm có hoành độ dương và đồ thị hàm số y= f’ ( x) cho bởi hình vẽ bên. Tìm phần nguyên của giá trị diện tích hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
A. 2.
B. 27.
C. 29.
D. 35.