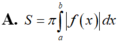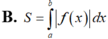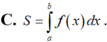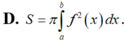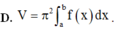Các câu hỏi tương tự
Cho hàm số y f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số y f)x), trục hoành và hai đường thẳng xa; xb (ab). Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức
Đọc tiếp
Cho hàm số y =f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số y = f)x), trục hoành và hai đường thẳng x=a; x=b (a<b). Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức
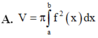
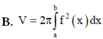
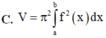

Cho hàm số y f(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y f(x) trục hoành và hai đường thẳng x a; xn Thể tích của khối của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x =a; x=n Thể tích của khối của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:

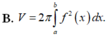
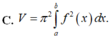
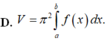
Cho hàm số yf(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số yf(x), trục hoành và hai đường thẳng xa;xb (a,b)Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức
Đọc tiếp
Cho hàm số y=f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a;x=b (a,b)Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức

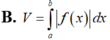
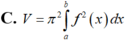
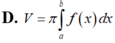
Cho hàm số y f(x) liên tục trên đoạn [a;b] và f(x)0 Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y f(x) trục hoành và 2 đường thẳng xa; xb Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b] và f(x)>0 Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và 2 đường thẳng x=a; x=b Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
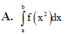
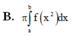
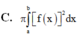
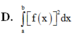
Cho hàm số y f(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y f(x) trục hoành và hai đường thẳng xa; xb. Diện tích hình phẳng D được tính bởi công thức.
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x=a; x=b. Diện tích hình phẳng D được tính bởi công thức.
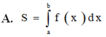
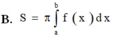
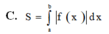
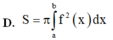
Thể tích của khối tròn xoay được giới hạn bởi đồ thị hàm số
y
f
(
x
)
liên tục trên đoạn [a;b] trục Ox và hai đường thẳng
x
a
,
x
b
quay quanh trục Ox, có công thức là: A.
V
∫
a
b
f
2...
Đọc tiếp
Thể tích của khối tròn xoay được giới hạn bởi đồ thị hàm số y = f ( x ) liên tục trên đoạn [a;b] trục Ox và hai đường thẳng x = a , x = b quay quanh trục Ox, có công thức là:
A. V = ∫ a b f 2 x d x
B. V = π ∫ a b f 2 x d x
C. V = π ∫ a b f x d x
D. V = π ∫ a b f x d x
Cho hàm số y f(x) liên tục trên đoạn [a;b]. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y f(x) trục hoành và hai đường thẳng xa; xb (ab) được tính theo công thức:
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b]. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) trục hoành và hai đường thẳng x=a; x=b (a<b) được tính theo công thức:
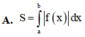
![]()
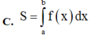
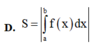
Cho hàm số y f(x) liên tục trên [a, b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y f(x), trục hoành và hai đường thẳng x a; x b được tính theo công thức
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a, b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được tính theo công thức
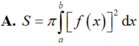
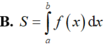
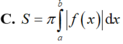

Cho hàm số f(x) liên tục trên R diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
y
f
(
x
)
trục hoành và hai đường thẳng xa;xb (ab) được tính theo công thức
Đọc tiếp
Cho hàm số f(x) liên tục trên R diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = f ( x ) trục hoành và hai đường thẳng x=a;x=b (a<b) được tính theo công thức