Giả sử x là nghiệm của phương trình 4 l o g 2 x + x 2 = 8 . Tính ( l o g 3 x ) 3
A. 1
B. 8
C. 2 2
D. ± 1
Những câu hỏi liên quan
Giả sử
∫
2
x
+
3
x
(
x
+
1
)
(
x
+
2
)
(
x...
Đọc tiếp
Giả sử ∫ 2 x + 3 x ( x + 1 ) ( x + 2 ) ( x + 3 ) + 1 d x = - 1 g ( x ) + C (C là hằng số). Tính tổng của các nghiệm của phương trình g(x) = 0
A. –1
B. 1
C. 3
D. –3
Đáp án D
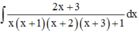
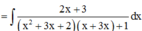
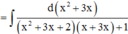
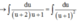
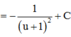
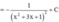
Suy ra tổng của các nghiệm của phương trình g(x) = 0 là - 3
Đúng 0
Bình luận (0)
Giả sử
∫
2
x
+
3
x
(
x
+
1
)
(
x
+
2
)
(
x
+
3
)
+
...
Đọc tiếp
Giả sử ∫ 2 x + 3 x ( x + 1 ) ( x + 2 ) ( x + 3 ) + 1 d x = - 1 g ( x ) + C (C là hằng số). Tính tổng của các nghiệm của phương trình g(x) = 0
A. -1
B. 1
C. 3
D. -3
Giả sử x là nghiệm của phương trình 4 1 x - 2 = ln e 2 . Tính lnx
A. 0
B. ln3
C. -ln3
D. 1
Để ý rằng
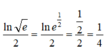
nên phương trình đã cho tương đương với
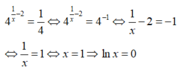
Chọn đáp án A.
Đúng 0
Bình luận (0)
Cho phương trình x2-(m+4)x+m2+2m-1=0.Giả sử x0 là nghiệm của phương trình đã cho . Tính giá trị lớn nhất, giá trị nhỏ nhất của x0
b1 :Giả sử x1 và x2 là nghiệm của phương trình \(x^2-2(m-1)x+m^2-1=0\). Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
b2: :Giả sử x1 và x2 là nghiệm của phương trình \(x^2-2(m-1)x+m^2-3m=0\). Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
Bài 1:
Với $x_1,x_2$ là hai nghiệm của phương trình đã cho, ta áp dụng hệ thức Viete có: \(\left\{\begin{matrix} x_1+x_2=2(m-1)\\ x_1x_2=m^2-1\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} x_1+x_2+2=2m\\ x_1x_2+1=m^2\end{matrix}\right.\)\(\Rightarrow \left\{\begin{matrix} (x_1+x_2+2)^2=4m^2\\ 4(x_1x_2+1)=4m^2\end{matrix}\right.\)
\(\Rightarrow (x_1+x_2+2)^2=4(x_1x_2+1)\)
\(\Leftrightarrow x_1^2+x_2^2+2x_1x_2+4(x_1+x_2)+4=4x_1x_2+4\)
\(\Leftrightarrow x_1^2+x_2^2-2x_1x_2+4(x_1+x_2)=0\)
Đây chính là hệ thức cần tìm
Đúng 0
Bình luận (0)
Bài 2:
Áp dụng hệ thức Viete ta có: \(\left\{\begin{matrix} x_1+x_2=2(m-1)\\ x_1x_2=m^2-3m\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} x_1+x_2+2=2m(1)\\ x_1x_2=m^2-3m\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} (x_1+x_2+2)^2=4m^2\\ 4x_1x_2=4m^2-12m\end{matrix}\right.\) \(\Rightarrow 12m=(x_1+x_2+2)^2-4x_1x_2(2)\)
Từ \((1); (2)\Rightarrow (x_1+x_2+2)^2-4x_1x_2=6(x_1+x_2+2)\)
\(\Leftrightarrow x_1^2+x_2^2-2x_1x_2-2(x_1+x_2)-8=0\)
Đây chính là biểu thức cần tìm.
Đúng 0
Bình luận (1)
Cho hệ phương trình
5
x
+
2
y
-
3
3
x
+...
Đọc tiếp
Cho hệ phương trình 5 x + 2 y = - 3 3 x + y = - 2
Giả sử (x;y) là nghiệm của hệ phương trình, khi đó - x . y 3 bằng
A. -1.
B. 1
C. 2
D. -2
giả sử a,b là nghiệm của phương trình \(x^2+px+1=0\)
giả sử c,d là nghiệm của phương trình \(x^2+qx+1=0\)
chứng minh hệ thức: (a-c)(a+d)(b+d)=\(q^2-p^2\)
giả sử (x0,y0) là nghiệm của hệ phương trình \(\left\{{}\begin{matrix}x^2+y^2=25\\x+y-xy=-5\end{matrix}\right.\)
Cho hệ phương trình
x
+
y
+
1
+
1
4
x
+
y
2
+
3...
Đọc tiếp
Cho hệ phương trình x + y + 1 + 1 = 4 x + y 2 + 3 . x + y 2 x - y = 3 2 .Giả sử (x;y) là cặp nghiệm của hệ phương trình. Khi đó, A = 9x2 – 12y + 1 bằng
A. 3
B. 9
C. 4
D. 7
