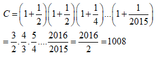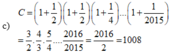Tính nhanh: (12015 - 1012015)x(22015 - 1002015)x(32015 - 992015)x ... x(1012015 - 12015)

Những câu hỏi liên quan
Chứng minh rằng: 12015 + 22015 + ..... + 20152015 chia hết cho 1 + 2 + ... + 2015.
tìm gtln của
F=\(x+x^2+x^3+...+x^12015+2015(1+x^12015)\)
x<=0
giup minh voi
3x+3 . 2 = 53+37 . 12015
GIÚP EM NHANH VỚI Ạ
\(3^{x+3}\cdot2=5^3+37\cdot1^{2015}\\\Rightarrow3^{x+3}\cdot2=125+37\\\Rightarrow3^{x+3}\cdot2=162\\\Rightarrow3^{x+3}=162:2\\\Rightarrow3^{x+3}=81\\\Rightarrow3^{x+3}=3^4\\\Rightarrow x+3=4\\\Rightarrow x=4-3\\\Rightarrow x=1\)
Đúng 3
Bình luận (0)
\(3^{x+3}.2=5^3+37.1^{2015}\\ 3^{x+3}.2=125+37.1=125+37=162\\ 3^{x+3}=\dfrac{162}{2}=81=3^4\\ Nên:x+3=4\\ Vậy:x=4-3=1\)
Đúng 2
Bình luận (0)
3\(x+3\).2 = 53 + 37.12015
3\(x\).27.2 = 125 + 37
3\(^x\).54 = 162
3\(^x\) = 162 : 54
3\(^x\) = 3
\(x\) = 1
Đúng 0
Bình luận (0)
Tính
C
1
+
1
2
1
+
1
2
1
+
1
4
.
.
.
1
+
1
2015
Đọc tiếp
Tính
C = 1 + 1 2 1 + 1 2 1 + 1 4 . . . 1 + 1 2015
Tính
c) C = 1 + 1 2 1 + 1 2 1 + 1 4 . . . 1 + 1 2015
A=1/15+1/35+1/63+1/99+......+12015+1/3135
\(A=\frac{1}{3\cdot5}+\frac{1}{5\cdot7}+...+\frac{1}{55\cdot57}\)
\(2A=\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{55}-\frac{1}{57}\)
\(2A=\frac{1}{3}-\frac{1}{57}\)
\(2A=\frac{6}{19}\)
\(A=\frac{3}{19}\)
Đúng 0
Bình luận (0)
Ta có:
A=1/15+1/35+1/63+1/99+...+1/2015+1/3135
=1/3.5+1/5.7+1/7.9+1/9.11+...+1/45.47+1/47.49
=1/3-1/5+1/5-1/7+1/7-1/9+...+1/45-1/47+1/47-1/49
=1/3-1/49
=49/147-3/147
=47/147
Đúng 0
Bình luận (0)
\(A=\frac{1}{12}+\frac{1}{35}+\frac{1}{63}+\frac{1}{99}+...+\frac{1}{2015}+\frac{1}{3135}\)
\(A=\frac{1}{3\cdot5}+\frac{1}{5\cdot7}+\frac{1}{7\cdot9}+\frac{1}{9\cdot11}+...+\frac{1}{45\cdot47}+\frac{1}{47\cdot49}\)
\(A=\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{47}-\frac{1}{49}\)
\(A=\frac{1}{3}-\frac{1}{49}\)
\(A=\frac{46}{147}\)
\(49-3=46\text{ nha bạn !}\)
Đúng 0
Bình luận (0)
Giải các bất phương trình sau:a)
x
+
2
6
+
x
+
5
3
x
+
3
5
+
x
+
6
2
b)
x
−...
Đọc tiếp
Giải các bất phương trình sau:
a) x + 2 6 + x + 5 3 > x + 3 5 + x + 6 2
b) x − 2 1007 + x − 1 1008 < 2 x − 1 2017 + 2 x − 3 2015
Giải bất phương trình sau:
2
x
−
5
2013
+
x
−
2
1007
≤
2
x
−
3
2015
+
x
−
1
1008
Đọc tiếp
Giải bất phương trình sau: 2 x − 5 2013 + x − 2 1007 ≤ 2 x − 3 2015 + x − 1 1008
Cho x, y thoa man
X+2y/x+y=2016\32015
tìm x:
2x + 1 . 22014= 22015
\(2^{x+1}\cdot2^{2014}=2^{2015}\\ 2^{x+1}=2^{2015}:2^{2014}\\ 2^{x+1}=2\\ =>x+1=1\\ x=1-1\\ x=0\)
Đúng 2
Bình luận (3)