Tìm a để diện tích hình phẳng giới hạn bởi đường cong y = 3 x đường thẳng x = 1 đường thẳng x = 1 a > 1 bằng 3.
A. 3e
B. e 2
C. e
D. 2e
Những câu hỏi liên quan
Tìm a để diện tích hình phẳng giới hạn bởi đường cong
y
3
x
,
đường thẳng
x
1
đường thẳng
x
a
a
1
bằng 3. A. 3e B. e C. 2e D.
e
2
Đọc tiếp
Tìm a để diện tích hình phẳng giới hạn bởi đường cong y = 3 x , đường thẳng x = 1 đường thẳng x = a a > 1 bằng 3.
A. 3e
B. e
C. 2e
D. e 2
Tìm a để diện tích hình phẳng giới hạn bởi đường cong
y
3
x
đường thẳng x1 đường thẳng xa (a1) bằng 3.
Đọc tiếp
Tìm a để diện tích hình phẳng giới hạn bởi đường cong y = 3 x đường thẳng x=1 đường thẳng x=a (a>1) bằng 3.
Biết diện tích hình phẳng giới hạn bởi đường cong yf(x), y0, x2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong yf(2x), trục hoành Ox và hai đường thẳng x0, xa bằng:
Đọc tiếp
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
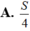
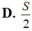
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
Diện tích hình phẳng giới hạn bởi đường thẳng y=x+3 , đường cong y=x^2+1 là
Phương trình hoành độ giao điểm:
\(x^2+1=x+3\Leftrightarrow x^2-x-2=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
\(S=\int\limits^2_{-1}\left|x^2-x-2\right|dx=\int\limits^2_{-1}\left(-x^2+x+2\right)dx=\left(-\dfrac{1}{3}x^3+\dfrac{1}{2}x^2+2x\right)|^2_{-1}=\dfrac{9}{2}\)
Đúng 1
Bình luận (0)
Tính diện tích hình phẳng giới hạn bởi đường cong y = x 2 - x + 3 và đường thẳng y=2x+1
A. 1/3
B. 1/6
C. 1/4
D. 1/2
Diện tích hình phẳng giới hạn bởi đường cong yf(x), trục hoành và hai đường thẳng x0; x1 là A.
π
∫
0
1
f
2
x
d
x
B.
∫
0
1
f
2
x
d
x
B.
∫
0
1
f
x...
Đọc tiếp
Diện tích hình phẳng giới hạn bởi đường cong y=f(x), trục hoành và hai đường thẳng x=0; x=1 là
A. π ∫ 0 1 f 2 x d x
B. ∫ 0 1 f 2 x d x
B. ∫ 0 1 f x d x
D. ∫ 0 1 f x d x
Diện tích hình phẳng giới hạn bởi các đường cong y sin x; y cos x và các đường thẳng
x
0
,
x
π
bằng A.
3
2
B.
2
C.
2
2
D. -
2
2
Đọc tiếp
Diện tích hình phẳng giới hạn bởi các đường cong y = sin x; y= cos x và các đường thẳng x = 0 , x = π bằng
A. 3 2
B. 2
C. 2 2
D. - 2 2
Đáp án C
Giải phương trình: s inx = cos x ⇒ x = π 4 (vì 0 ≤ x ≤ π )
S = ∫ 0 π s inx − cos x d x = 2 2
Đúng 0
Bình luận (0)
Diện tích hình phẳng giới hạn bởi đường cong
y
2
x
và đường thẳng
x
1
bằng S là A.
S
1
3
B.
S
4
3
C.
S
2
3
D.
S
1
6
Đọc tiếp
Diện tích hình phẳng giới hạn bởi đường cong y 2 = x và đường thẳng x = 1 bằng S là
A. S = 1 3
B. S = 4 3
C. S = 2 3
D. S = 1 6
